PUCRIO – Física 1 – 2020.1 – P2 – M. Escolha
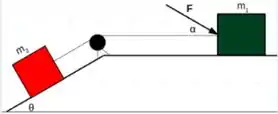
. Na figura, o bloco tem peso e bloco tem peso e está sobre uma rampa que faz com a horizontal. Uma força com módulo é aplicada sobre o bloco fazendo um ângulo de com a horizontal. Considere que não existe atrito entre os blocos e as superfícies e que a corda e a polia são ideias. Determine a aceleração dos blocos e determine se o bloco está subindo ou descendo a rampa. Considere .
Passo 1
Vem comigo que a gente resolve essa juntos.
A primeira coisa a se ligar é que como os blocos estão ligados por uma corda ideal que passa por uma polia ideal, eles tem a mesma aceleração.
Para determinar essa aceleração vamos usar a segunda lei de Newton ao nosso favor. Como estamos interessados na aceleração, vamos analisar somente as direções onde temos força resultante nos blocos.
Então vamos as contas!
Passo 2
Vamos começar com o bloco , o diagrama de corpo livre desse bloco é da seguinte forma:
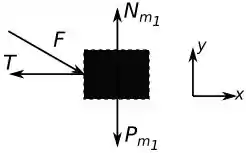
Usando a segunda lei de Newton na direção , vamos considerar que esse bloco esteja indo para direita, assim temos:
Passo 3
Agora vamos analisar o bloco , o diagrama de corpo livre desse bloco é da seguinte forma:
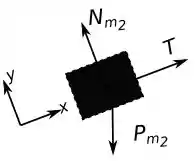
Usando a segunda lei na direção , temos:
Passo 4
Como já tínhamos visto no passo , as acelerações são iguais, logo:
O enunciado nos dá o valor da força peso dos blocos, usando que:
Temos que:
Isolando , temos:
Substituindo os valores que conhecemos, temos:
Passo 5
Usando esse resultado na equação que chegamos no passo , poderemos encontrar a aceleração. Então:
Com isso temos que:
Como essa aceleração é positiva, a nossa suposição do bloco está indo para a direita está certa, então o bloco está subindo.
Resposta
O bloco está subindo.