Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 2012345678910111213141516171819212223242526272829

Enunciado

PUCRIO – Física 1 – 2020.1 – P2 – M. Escolha

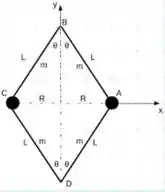
10 . O sistema mostrado na Figura é formado por quatro barras iguais de massa m = 100   g e comprimento L = 30,00   c m e por duas massas pontuais iguais de massa M = 400   g presas às barras nos pontos A e C . Sabe-se que o momento de inércia de uma barra que forma um o ângulo θ com o eixo de rotação que passa pelo seu centro de massa é I C M = m L sen ⁡ θ 2 / 12 , R = L sen ⁡ θ = 15,00   c m . Determine o momento de inércia do sistema em torno do eixo y .

Passo 1

Vem comigo que a gente detona com essa questão!

Então temos que calcular o momento de inércia desse sistema. Para saber o momento desse sistema precisamos saber o momento de cada peça que o compõe e somá-los.

O momento de inércia das massas pontuais é dado por:

I M = M r 2

Onde r é a distância entre a massa e o eixo de rotação.

Para achar o momento das barras em relação ao eixo de rotação vamos usar o teorema dos eixos paralelos, já que o enunciado nos deu momento de inércia de uma barra referente a um eixo que passa pelo seu centro de massa.

O teorema dos eixos paralelos é dado por:

I = I C M + m d 2

Onde I C M é o momento de inércia que já conhecemos e d a distância entre os eixos.

Como todas as barras são iguais e tem a mesma distância do eixo de rotação, basta calcular o momento de inércia de uma delas e depois multiplicá-lo por 4 .

Vamos as contas então!

Passo 2

Vamos primeiro calcular o momento de inércia das massas pontuais, como elas são iguais e tem a mesma distância do eixo de rotação, basta calcular de uma e depois multiplicar o resultado por 2 .

Temos que:

I M = M r 2

⇒ I M = M R 2

Substituindo com os valores que conhecemos, temos:

I M = 0,4 0,15 2

⇒ I M = 0,009

Então o momento de inércia das duas barras é:

2 I M = 0,018

Passo 3

Vamos agora calcular o momento de inércia de uma das barras, temos:

I = I C M + m d 2

⇒ I = m L sen ⁡ θ 2 12 + m R 2 2

⇒ I = m R 2 12 + m R 2 2

Substituindo com os valores que conhecemos, temos:

I = 0,1 0,15 2 12 + 0,1 0,15 2 2

= 0,0001875 + 0,0005625

Assim temos que:

⇒ I = 0,00075

Então o momento das quatro barras é dado por:

4 I = 0,003

Passo 4

Podemos encontrar o momento de inércia total, temos:

I T = 2 I M + 4 I

⇒ I T = 0,018 + 0,003

Logo temos que:

I T = 0,021 = 2,1 × 10 - 2 k g ⋅ m 2

E finalizamos a questão!

Resposta

I T = 2,1 × 10 - 2 k g ⋅ m 2

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.