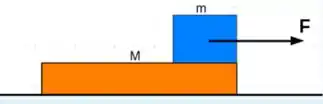
. A figura ilustra um bloco de massa sobre uma prancha de massa apoiada sobre um piso horizontal perfeitamente liso. Considere o coeficiente de atrito estático entre o bloco e a prancha. Determine o maior valor possível do módulo de que permita movimento solidário dos dois corpos (sem deslizamento relativo) e indique quais são pares ação reação entre o bloco e a prancha.
Passo 1
Vem comigo que a gente detona com esse problema!
Temos que encontrar qual a maior força que faz com que os blocos andem juntos, sem um deslizar em relação ao outro.
Para ficar mais claro para gente que forças temos atuando nesse sistema, e fazermos uma análise melhor, vamos desenhar o diagrama de corpo livre de cada bloco. Temos:
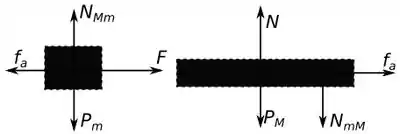
Onde temos que e , já que são pares de ação e reação.
O detalhe que vai nos ajudar a resolver esse problema é o fato de que como os blocos tem que se deslocar juntos, eles tem que ter a mesma aceleração.
Então o termo da aceleração da força resultante na direção horizontal de cada bloco deve ser igual.
Vamos então usar a segunda lei de Newton ao nosso fator.
Passo 2
Vamos começar com o bloco de massa . Vamos primeiro usar a segunda lei na direção vertical, temos:
Usando que , temos:
Agora fazendo a análise na horizontal, temos:
Essa força de atrito é dada por:
Onde , assim:
Então temos que:
Passo 3
Agora vamos analisar a prancha de massa . Podemos começar com a direção horizontal, temos:
Usando o que já sabemos de , temos:
Podemos então igualar as expressões que temos para a aceleração.
Passo 4
Então temos que:
Então temos que:
Então essa é a força de que precisamos.
Resposta
As forças que formam par de ação e reação entre o bloco e a prancha é a força normal entre eles e a força de atrito entre eles .