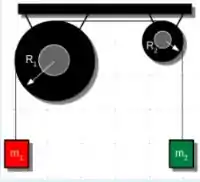
. Os cilindros mostrados na Figura têm raios e , massas e e momentos de inércia em relação a seus centros de massa determinados pela relação geral . Os cilindros são livres para girar em torno de eixos horizontais fixos, perpendiculares à figura e que passam pelos respectivos centros de massa. O fio de massa desprezível passa sem deslizamento pelos cilindros e suas pontas livres estão presas a corpos de massas e , em repouso na mesma altura. Determine a aceleração dos corpos e a velocidade do corpo quando este se deslocou . Adote .
Passo 1
Vem comigo que a gente detona essa questão juntos!
Para esse problema teremos que avaliar as forças resultantes que agem nos corpos e nos cilindros teremos que avaliar o torque resultante (Como se fosse a força resultante, mas no caso de rotação de corpos)
Avaliando essas equações da força resultante e de torque resultante poderemos manipulá-las para poder tirar a aceleração dos blocos, que vai ser a mesma já que o fio que os liga é sem massa e passa pelas polias sem deslizar.
Depois que encontrarmos essa aceleração, podermos achar a velocidade do corpo no deslocamento de que ele teve, vamos usar a seguinte equação:
Onde , já que ele parte do repouso e .
Vamos as contas então!
Passo 2
Vamos começar com o corpo , e vamos supor que ele está descendo já que sua massa é maior, a força resultante sobre ele é dada por:
Onde é a tenção que essa parte do fio causa sobre ele.
Agora para , temos que ele está subindo já que está descendo, assim:
Onde é a tensão que ele sofre dessa parte do fio ligado a ele.
Passo 3
Agora vamos achar o torque resultante sobre o cilindro , temos o seguinte:
Onde consideramos o sentido de rotação anti-horário como sendo o positivo.
A tensão é referente a parte do fio que liga os dois cilindros.
Usando que a aceleração angular é , temos:
Agora vamos ver o torque resultante sobre o cilindro , temos o seguinte:
Assim temos que:
Passo 4
Então encontramos as seguintes equações:
Vamos então dividir as duas últimas por e respectivamente, depois somar as quatro, com isso temos:
Usando os momentos de inércia de cada cilindro, temos:
Substituindo os valores que temos, ficamos com:
Essa é a aceleração dos corpos.
Passo 5
Agora vamos encontrar a velocidade de quando ele se deslocou , usando a equação que vimos no passo , temos:
Substituindo com o que sabemos, temos:
Com isso temos que:
Finalizamos a questão com sucesso!