UnB – Física 1 – Listas – Lista de Exercícios Física 1 UnB – Lista 7 – Trabalho e Energia Cinética – 7
Um professor de física está sentado em sua cadeira, que desliza sobre rolamentos sem atrito, sendo empurrado para cima de um plano inclinado a acima da horizontal. A massa total do professor com sua cadeira é igual a . Ele é empurrado ao longo do plano inclinado por um grupo de alunos que juntos exercem uma força horizontal constante de . O professor possuía uma velocidade de na base da rampa. Use o teorema do trabalho-energia cinética para calcular sua velocidade no topo da rampa.
Passo 1
Eaee!!! Belezinha? Olha.. basicamente nessa questão temos um prof bem brincalhão que ensina Física de modo super divertido com seus alunos haha. Eles vão empurrar o professor em uma rampa e, com isso, vão verificar a velocidade no final da rampa utilizando o teorema de trabalho e energia cinética!!!
Aí eu te pergunto: Como relacionar trabalho com energia cinética???
Pois bem... é o seguinte... o trabalho também é dado como a variação da energia cinética, ou seja:
Mas antes de aplicar, vamos verificar direitinho a situação!
Passo 2
Na cadeira, vemos que as forças que estão no sentido do deslocamento são as componentes de e (força peso) ... como podemos ver na figura abaixo:
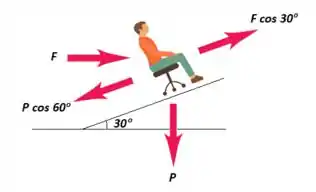
Como as forças são contrárias, podemos determinar o trabalho por:
Passo 3
Dessa forma, temos que a velocidade no final da rampa é dada por:
Entendeu direitinho? Responde aee ;)
