Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica

Ver Teoria
Exercício 361234567891011121314151617181920212223242526272829303132333435373839404142434445464748495051525354555657585960616263646566

Enunciado

UnB – Física 1 – Listas – Lista de Exercícios Física 1 UnB – Lista 7 – Trabalho e Energia Cinética – 8a

Um bloco de 5.0   k g se move com uma velocidade de v 0   =   6.0 m / s sobre uma superfície horizontal sem atrito, dirigindo-se contra uma mola cuja constante elástica é dada por k   =   500 N / m e que possui uma de suas extremidades presa a uma parede (ver figura abaixo).

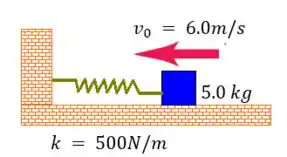
a) Calcule a distância máxima que a mola pode ser comprimida.

Passo 1

Eaee!!! Belezinha? Olha.. o bloco começará com uma velocidade e vai se encontrar com uma mola. Daqui já podemos prever que iremos utilizar a conservação de energia!!

Dessa forma, a questão nos pede a distância máxima que a mola pode ser comprimida.

Aí eu te pergunto: Como vamos relacionar tudo isso?

Pois bem... é o seguinte... pela conservação da energia, a energia inicial (cinética) será igual a energia final (potencial elástica), ou seja:

E c = E e l

Agora vamos aplicar!!

Passo 2

Assim, temos que:

E c = E e l ∴

m v 2 2 = k x 2 2 ∴

5 ∙ 6 2 = 500 ∙ x 2 ∴

x = 0,6   m

Entendeu direitinho? Responde aee ;)

Resposta

x = 0,6   m

Exercícios de Livros Relacionados

A Fig. 8-39a se refere à mola de uma espingarda de rolha (Fig. 8-39b); ela mostra a força da mola em função da distensão ou compressão da mola. A mola é comprimida 5,5c m e usada para impulsionar uma
Uma mola com uma constante elástica de 3200N / m é distendida até que a energia potencial elástica seja 1,44J . ( U = 0 para a mola relaxada.) Quanto é ∆ U se a distensão muda para (a) uma distensão d
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Em uma erupção vulcânica, um pedaço de 2k g de um rocha vulcânica porosa é jogada diretamente para cima com uma rapidez inicial de 40m / s . Ela viaja por uma distância de 50m antes de começar a cair