UnB – Física 1 – Listas – Lista de Exercícios Física 1 UnB – Lista 7 – Trabalho e Energia Cinética – 3c
Um pequeno bloco com massa de está ligado a um fio que passa através de um buraco em uma superfície horizontal sem atrito (figura abaixo). Inicialmente, o bloco gira a uma distância de do buraco com uma velocidade de . A seguir, o fio é puxado para baixo, fazendo o raio do círculo encurtar para . Nesta nova distância verifica-se que sua velocidade passa para .
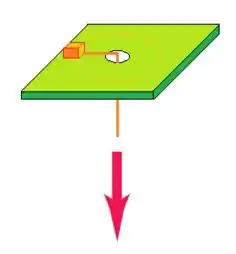
c) Qual foi o trabalho realizado pela pessoa que puxou o fio?
Passo 1
Eaee!!! Belezinha? Olha.. basicamente nessa questão temos um bloquinho girando em uma superfície com uma velocidade. Depois, quando puxou-se o fio para baixo, a velocidade do bloquinho aumentou.
No entanto, a questão nos pede o trabalho realizado pela pessoa que puxou o fio.
Aí eu te pergunto: Como podemos relacionar o trabalho com a “puxada” que a pessoa fez no bloquinho?
A resposta é basicamente uma das definições de trabalho, em que o trabalho exercido em um corpo é dado pela diferença de energia final e inicial, ou seja:
Nesse caso, é a diferença de energia cinética final e inicial!!!
Passo 2
Assim, temos que o trabalho é dado por:
Entendeu direitinho? Responde aee ;)
