Listas de Estudos pra Prova - Tipler Vol 1 - 6°ed de Física 1 da UTFPR - Movimento em Duas e Três Dimensões

(Cap 3 – Ex 69) (a) Quais são o período e a rapidez de uma pessoa em um carrossel, se a pessoa tem uma aceleração com magnitude de 0,80 m/s² quando situada a 4,0 m do eixo? (b) Quais são a magnitude de sua aceleração e sua rapidez, se ela se desloca até uma distância de 2,0 m ao centro do carrossel e o carrossel segue girando com o mesmo período?

(Cap 3 – Ex 51) Uma partícula tem um vetor posição dado por onde r está em metros e t em segundos. Encontre os vetores velocidade instantânea e aceleração instantânea como funções do tempo t.

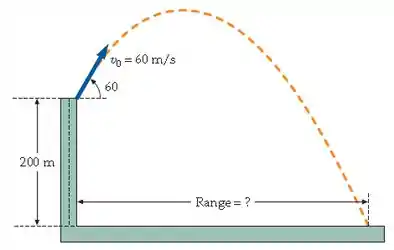
(Cap 3 – Ex 84) Um projétil é disparado do topo de uma colina de 200 m de altura, sobre um vale (Figura 3-36). Sua velocidade inicial é de 60 m/s, a 60° acima da horizontal. Onde o projeto cai? (Ignore a resistência do ar.)

(Cap 3 – Ex 52) Uma partícula tem uma aceleração constante No tempo t=0, a velocidade é zero e o vetor posição é . (a) Encontre os vetores velocidade e posição em função do tempo t. (b) Encontre a equação da trajetória da partícula no plano xy e esboce a trajetória.

(Cap 3 – Ex 66) Você está projetando uma centrífuga para girar a uma taxa de . (a) Calcule a máxima aceleração centrípeta que pode suportar um tubo de ensaio preso ao braço da centrífuga a do eixo de rotação. (b) A centrífuga leva e para atingir, a partir do repouso, sua taxa máxima de rotação. Calcule a magnitude da aceleração tangencial da centrífuga, suposta constante, enquanto ela está girando.

(Cap 3 – Ex 76) Um projétil é lançado do nível do chão com uma rapidez inicial de 53 m/s. Encontre o ângulo de lançamento (o ângulo que o vetor velocidade inicial forma acima da horizontal) de forma que a altura máxima do projétil seja igual ao seu alcance horizontal. (ignore a resistência do ar.)

(Cap 3 – Ex 50) No tempo zero, uma partícula está em x=4,0 m e y=3,0 m e tem a velocidade A aceleração da partícula é constante e dada por . (a) Encontre a velocidade em t= 2,0 s. (b) Expresse o vetor posição em t= 4,0 s em termos de Além disso, dê a magnitude e a orientação do vetor posição neste tempo.

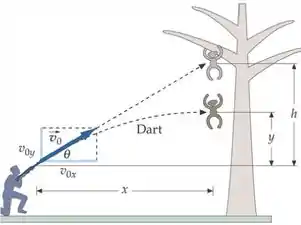
(Cap 3 – Ex 75) Na Figura 3-35, qual é a rapidez inicial mínima que o dardo deve ter para atingir o macaco antes que este chegue ao chão, que está abaixo da posição inicial do macaco, se e ? (Ignore a resistência do ar.)

(Cap 3 – Ex 110) Uma partícula se move no plano xy com aceleração constante.Em , a partícula está em , com a velocidade . Em , a partícula está em e com a velocidade . (a) Encontre . (b) Qual a aceleração da partícula? (c) Qual é a velocidade da partícula como função do tempo? (d) Qual é o vetor posição da partícula como função do tempo?

(Cap 3 – Ex 106) Consertando o telhado de sua casa, você deixa o martelo cair acidentalmente. O martelo escorrega pelo telhado a uma rapidez constante de 4,0 m/s. O telhado faz ângulo de 30° com a horizontal e seu ponto mais baixo está 10 m acima do chão. (a) Em quanto tempo, após abandonar o telhado, o martelo chega ao chão? (b) Qual é a distância horizontal percorrida pelo martelo, entre o instante em que abandona o telhado e o instante em que se choca com o chão? (Ignore a resistência do ar.)

(Cap 3 – Ex 83) Uma pedra, atirada horizontalmente do alto de uma torre de 24 m de altura, atinge o chão em um ponto que dista 18 m da base da torre. (a) Encontre a rapidez com que a pedra foi atirada. (b) Encontre a rapidez da pedra justo antes de atingir o chão.

(Cap 3 – Ex 99) Uma pedra é atirada do topo de um edifício de 20 m de altura a um ângulo de 53° acima da horizontal. (a) Se o alcance horizontal é igual à altura do prédio, com que rapidez a pedra foi atirada? (b) Quanto tempo ela fica no ar? (c) Qual é a velocidade da pedra justo antes de atingir o chão? (Ignore a resistência do ar.)

(Cap 3 – Ex 46) As coordenadas de posição (x,y) de uma partícula são (2,0 m, 3,0 m) em ; (6,0 m, 7,0 m) em ; e (13 m, 14 m) em (a) Encontre a magnitude da velocidade média de até (b) Encontre a magnitude da velocidade média de até

(Cap 3 – Ex 81) O Coiote (Carnivorus famelicus) está perseguindo o Papa-léguas (Ligeiribus ariscus). Na corrida, eles chegam a um profundo desfiladeiro, com 15,0 m de largura e 100 m de profundidade. Papa-léguas se lança a um ângulo de 15° acima da horizontal e chega do outro lado com 1,5 m de folga. (a) Qual a rapidez de lançamento do Papa-léguas? (b) O Coiote também pula para cruzar o desfiladeiro, com a mesma rapidez inicial, mas a um ângulo diferente. Para seu desespero, ele vê que erra o outro lado por 0,50 m. Qual foi seu ângulo de lançamento? (suponha este ângulo menor que 15°.)