Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lançamento Oblíquo

Ver Teoria
Exercício 891234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878890919293949596979899100

Enunciado

Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 3, Seção 1, Questão 75.

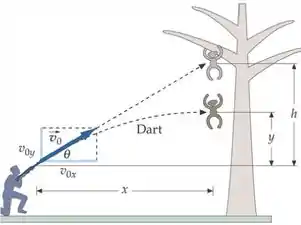
(Cap 3 – Ex 75) Na Figura 3-35, qual é a rapidez inicial mínima que o dardo deve ter para atingir o macaco antes que este chegue ao chão, que está 11,2   m abaixo da posição inicial do macaco, se x = 50   m e h = 10   m ? (Ignore a resistência do ar.)

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O problema nos pede a velocidade inicial mínima que o dardo deve ter para atingir o macaco que está caindo.

Se a velocidade for igual a essa velocidade mínima, então ele atinge o macaco quando o macaco está prestes a atingir o solo.

A componente horizontal da velocidade é dada por:

v 0 x = v x = v 0 cos ⁡ θ 0

v 0 = v x cos ⁡ θ 0

Vamos aplicar a definição de velocidade:

v x = ∆ x ∆ t

Portanto:

v 0 = ∆ x ∆ t ⋅ cos ⁡ θ 0

Dessa equação, já temos o ∆ x e o ângulo de lançamento. Então se a gente encontrar o tempo, achamos a velocidade.

Esse tempo vai vir justamente do fato de que queremos que o dardo chegue no macaco antes dele chegar no chão. Então vamos calcular o tempo que o macaco leva pra chegar no chão e substituir nessa equação aí em cima.

Passo 2

Agora vamos estudar o movimento do macaco. Sabemos que:

∆ h = 1 2 g ∆ t 2

Logo:

∆ t = 2 ∆ h g

Agora podemos substituir este tempo na equação da velocidade do dardo:

v 0 = ∆ x 2 ∆ h g ⋅ cos ⁡ θ 0

v 0 = ∆ x cos ⁡ θ 0 ⋅ g 2 ∆ h

Podemos descobrir o ângulo de lançamento, θ 0 , por trigonometria:

θ 0 = tan - 1 ⁡ 10 50 = 11,3 °

Portanto, temos que:

v 0 = 50   m cos ⁡ 11,3 ° ⋅ 9,81   m / s 2 2 ⋅ 11,2   m

v 0 = 34   m / s

Resposta

v 0 = 34   m / s

Exercícios de Livros Relacionados

Suponha que o ângulo inicial α 0 da Figura 3.26 seja 42,0 ° e que d seja igual a 3,0 m. Onde o dardo e o macaco se encontrarão, se a velocidade inicial do dardo for a) 12,0 m/s? b) 8,0 m/s?c) O que oc
Galileu mostrou que, se os efeitos da resistência do ar são ignorados, os alcances de projéteis (no mesmo nível) cujos ângulos de projeção diferem de 45°, para mais e para menos, do mesmo valor, são i
Em 1939 ou 1940 , Emanuel Zacchini levou seu número de bala humana a novas alturas: disparado por um canhão, passou por cima de três rodas-gigante antes de cair em uma rede (Fig.4-39). (a) Tratando Za
Os esquiadores experientes costumam dar um pequeno salto antes de chegarem a uma encosta descendente. Considere um salto no qual a velocidade inicial é v 0 =10m / s , o ângulo é θ 0 =9,0 ° , a pista a
Cortina da morte. Um grande asteroide metálico colide com a Terra e abre uma cratera no material rochoso abaixo do solo, lançando pedras para o alto. A tabela a seguir mostra cinco pares de velocidade