Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 3, Seção 1, Questão 81.
(Cap 3 – Ex 81) O Coiote (Carnivorus famelicus) está perseguindo o Papa-léguas (Ligeiribus ariscus). Na corrida, eles chegam a um profundo desfiladeiro, com 15,0 m de largura e 100 m de profundidade. Papa-léguas se lança a um ângulo de 15° acima da horizontal e chega do outro lado com 1,5 m de folga. (a) Qual a rapidez de lançamento do Papa-léguas? (b) O Coiote também pula para cruzar o desfiladeiro, com a mesma rapidez inicial, mas a um ângulo diferente. Para seu desespero, ele vê que erra o outro lado por 0,50 m. Qual foi seu ângulo de lançamento? (suponha este ângulo menor que 15°.)
Passo 1
a) Oi pessoal, tudo bem? Ele diz que o papaléguas se lança a um ângulo de e assim pula um desfiladeiro.
Na vertical temos a ação da gravidade, então teremos um movimento com aceleração constante. E na horizontal não há aceleração (desconsiderando a resistência do ar), então temos velocidade constante.
E esse bichinho chega no outro lado com uma folga de . Então ele passou do desfiladeiro de de largura e ainda chegou mais longe, de forma que seu alcance total foi:
E o enuncido quer saber a rapidez inicial dele. A figura abaixo retrata esse movimento do enunciado:
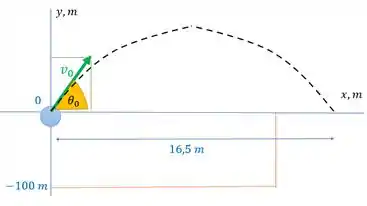
Como temos um movimento vertical independente do movimento horizontal, é uma boa escrever as componentes de :
Aí partir dessas informações e das equações referentes a cada tipo de movimento, vamos chegar no valor de . Bora lá!
Passo 2
Vamos começar equacionando o movimento horizontal. A gente tem a posição inicial e a final, e sabe que o movimento na horizontal tem velocidade constante. Logo vai ser a velocidade de todo o movimento. Por isso, a gente pode usar a equação:
Onde , e :
Agora vamos analisar o movimento vertical. Também temos a posição final e inicial. E sabemos que a acelaração é a da gravidade . Ela é negativa porque aponta para baixo.
Pensamos nessas coisas, a gente pode usar a equação horário da posição para constante:
Sabemos que a posição inicial e que a final também é (o papaléguas volta ao solo). Substituindo nossas informações e expressões na equação acima:
Lembrando que temos uma expressão para :
Passo 3
Percebe que a gente tem duas equações:
E temos duas incógnitas, e . Como queremos , vamos isolar a primeira equação e substituir na segunda:
Substituindo na segunda:
Isolando e resolvendo para a velocidade inicial, temos:
Substituindo os valores, temos:
Passo 4
b) Queremos o ângulo de lançamento do Coiote. O movimento dele vai ser quase igual ao do papaléguas. Temos a mesma rapidez inicial (que a gente achou no item anterior). Ele sai da posição e passa pela posição .
A diferença é que o alcance dele é menor. O enunciado diz que ele fica atrás do fim do desfiladeiro ao chegar em . Isso quer dizer que o alcance dele é de
E isso acontece porque o ângulo d salto dele é menor do que o do papaléguas. Precisamos descobrir esse ângulo .
Como a gente tem as mesmas posições finais e iniciais de e aqui também temos um movimento com aceleração constante na vertical e velocidade constante na horizontal, a gente pode usar a mesma expressão final que achamos para o item (a) que relaciona o alcance , ao ângulo e a rapidez inicial:
Isolando quem a gente quer:
Susbstituindo os valores, temos: