Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 3, Seção 1, Questão 99.
(Cap 3 – Ex 99) Uma pedra é atirada do topo de um edifício de 20 m de altura a um ângulo de 53° acima da horizontal. (a) Se o alcance horizontal é igual à altura do prédio, com que rapidez a pedra foi atirada? (b) Quanto tempo ela fica no ar? (c) Qual é a velocidade da pedra justo antes de atingir o chão? (Ignore a resistência do ar.)
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão. Temos uma pedra lançada sem resistência ao ar do alto de um prédio. Então na horizontal o movimento tem velocidade constante e na vertical temos aceleração constante (negativa pois a gravidade está para baixo).
A imagem a seguir pode nos ajudar a entender melhor o enunciado:
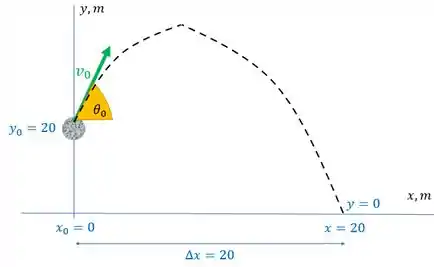
Sabemos que a altura do prédio é igual ao alcance da pedra, então . E ele quer saber a rapidez inicial dessa pedra .
Como os movimentos vertical e horizontal são independentes, a gente pode começar escrevendo a expressão das componentes da velocidade inicial: e
Aí partir dessas informações e das equações referentes a cada tipo de movimento, vamos chegar no valor de . Bora lá!
Passo 2
Vamos começar equacionando o movimento horizontal. A gente tem o deslocamento, e sabe que o movimento na horizontal tem velocidade constante. Logo vai ser a velocidade de todo o movimento. Por isso, a gente pode usar a equação:
Onde :
Agora vamos analisar o movimento vertical. Também temos o deslocamento. E sabemos que a acelaração é a da gravidade . Pensamos nessas coisas, a gente pode usar a equação horário da posição para aceleração constante:
Lembrando que temos uma expressão para e :
Passo 3
Percebe que a gente tem duas equações:
E temos duas incógnitas, e . Como queremos , vamos isolar a primeira equação e substituir na segunda:
Substituindo na segunda:
Como e , temos que:
Isolando e substituindo os valores, temos:
Passo 4
b) Cara, a gente viu no passo 2 que horizontalmente, temos a seguinte equação
Então a gente pode achar o tempo de vôo por essa equação. Vamos substituir nossos dados:
Passo 5
c) Agora temos que encontrar as componentes da velocidade final da pedra, para expressar a velocidade dela ao atingir o chão, ou seja, no momento que chega ao solo, na forma de vetor.
A componente horizontal é a mesma durante todo o movimento porque essa direção a velocidade é constante. Então podemos dizer que
Já para a vertical, podemos usar a equação horária da velocidade para aceleração constante:
Sendo que e :
Substituindo os dados:
A velocidade final será:
Obs: as respostas do gabaritos estão mais arredondadas, mas estamos certinhos aqui também, tá?