(Cap 3 – Ex 106) Consertando o telhado de sua casa, você deixa o martelo cair acidentalmente. O martelo escorrega pelo telhado a uma rapidez constante de 4,0 m/s. O telhado faz ângulo de 30° com a horizontal e seu ponto mais baixo está 10 m acima do chão. (a) Em quanto tempo, após abandonar o telhado, o martelo chega ao chão? (b) Qual é a distância horizontal percorrida pelo martelo, entre o instante em que abandona o telhado e o instante em que se choca com o chão? (Ignore a resistência do ar.)

Oi galera, tudo bem? Vamos tentar visualizar o problema através da figura abaixo:

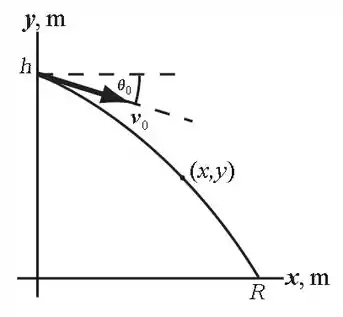
De acordo com o enunciado, podemos notar que o martelo está escorregando pelo telhado a uma velocidade constante. Depois que ele sai do telhado, acontece o movimento da figura e é importante saber o que é cada um desses dados.

Pensa comigo, o martelo está escorregando a velocidade constante no telhado, então, a velocidade inicial com que o martelo abandona o telhado é a mesma com a qual ele escorregava. E como o telhado forma um ângulo de 30° com a horizontal, então o martelo tbm abandona o telhado a 30° da horizontal, pois ele tende a seguir o movimento.

Certo, agora que já destrinchamos a questão é só resolver.

Queremos então, encontrar o tempo que o martelo leva pra atingir o chão depois de abandonar o telhado.

Para isso devemos usar uma equação que se adeque aos nossos dados.

Podemos usar Torricelli para descobrir a velocidade final do movimento, e com a velocidade final fica fácil de achar nosso tempo. Vamos lá!!!

É importante visualizar que nós estamos indo de uma altura inicial para uma altura final , então nosso .

Com a velocidade de chegada ao chão encontrada podemos descobrir o tempo através da equação:

Ficou confuso com os sinais adotados? É só tentar visualizar... Estamos trabalhando com vetores e adotamos sentido positivo em x e y positivos.