Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Torque

Ver Teoria
Exercício 135123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 9, Seção 1, Questão 110.

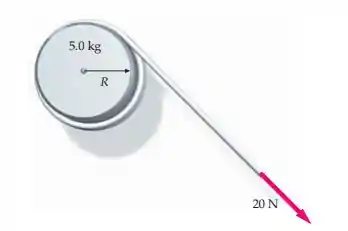
(Cap 9 – Ex 110) Um disco uniforme de 5,0 k g tem um raio de 0,12 m e gira livremente em torno de seu eixo. Um cordão, enrolado em volta do disco, é puxado com uma força de 20 N . (a) Qual é o torque exercido por esta força em relação ao eixo de rotação? (b) Qual é a aceleração angular do disco? (c) Se o disco parte do repouso, qual é sua rapidez angular após 5,0 s ? (d) Qual é a energia cinética após os 5,0 s ? (e) Qual é o deslocamento angular do disco durante os 5,0 s ? (f) Mostra que o trabalho realizado pelo torque, τ Δ θ , é igual à energia cinética.

Passo 1

Falaiiii galerinha do Responde ai, tudo certinho?

Bora resolver essa juntinhooos?

Sabemos que temos infinitas letras pra resolver, mas fica tranquilo que são bem simples.

O enunciado nos fornece alguns dados importantíssimos para essa resolução, bora retirar eles

Raio do disco é 0.12m,

Massa do disco é 5 kg,

Força aplicada no disco é 20 N.

  1. Vamos usar a definição de torque:

    2. τ = F R = 20 N 0.12 m

    τ = 2.4   N ⋅ m

    Passo 2

  2. Agora, pela segunda lei de Newton, e conhecendo o momento de inércia do disco:

    3. τ = I α

    α = τ M R 2 2

    = 2 τ M R 2

    Substituindo valores:

    α = 2 × 2.4 5 × 0.12 2

    α = 66.7   r a d / s 2

    Passo 3

  3. Agora que conhecemos a aceleração angular, vamos achar a velocidade angular:

    4. ω = ω 0 + α t = 0 + α t

    ω = 66.7 × 5

    ω = 333 r a d s

    ω = 3.3 × 10 2 r a d s

    Passo 4

  4. A energia rotacional é calculada por:

    5. K r o t = I ω 2 2

    = M R 2 2 ω 2 2

    K r o t = M R 2 ω 2 4

    K r o t = 1 4 5 × 0.12 2 × 333 2

    K r o t = 2.0 k J

    Passo 5

  5. Como está acelerado e partindo do repouso, o deslocamento angular vai ser:

    6. Δ θ = α t 2 2

    = 66.7 × 5 2 2

    Δ θ = 8.3 × 10 2   r a d

    Passo 6

  6. Na expressão da energia rotacional, vamos substituir:

τ = I α

I = τ α

ω = α t

K = I ω 2 2 = τ α α t 2 2

= 1 2 α τ t 2

= τ × 1 2 α t 2

K = τ Δ θ

Resposta

  1. τ = 2.4   N ⋅ m
  2. α = 66.7   r a d / s 2
  3. ω = 3.3 × 10 2 r a d s
  4. K r o t = 2.0 k J
  5. Δ θ = 8.3 × 10 2   r a d

Exercícios de Livros Relacionados

Em uma rasteira de judô, você tira o apoio do pé esquerdo do adversário e, ao mesmo tempo, puxa seu quimono para o lado sem apoio. Em consequência, o lutador gira em torno do pé direito e cai no tatam
Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/s2, qual é o momento de inércia da roda?
Duas forças agem sobre um corpo. Quais das seguintes afirmações estão corretas?(a) O corpo está em equilíbrio se as forças são iguais em módulo e contrárias em direção.(b) O corpo está em equilíbrio s
Uma polia, com um momento de inércia de 1,0 X 10- 3 kg · m2 em relação ao eixo e um raio de 10 cm, é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo
Na figura abaixo, um cilindro com uma massa de 2,0k g pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F → 1 = 6,0N , F → 2 = 4,0N , F → 3 = 2