Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 10, Seção 1, Questão 63.
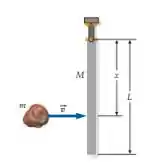
(Cap 10 – Ex 63) A Figura 10-53 mostra uma barra fina e uniforme, de comprimento e massa , articulada na extremidade superior. A barra, que está inicialmente em repouso, é atingida por uma partícula de massa no ponto abaixo da articulação. Suponha que a partícula grude na barra. Qual deve ser a rapidez da partícula, de forma que após a colisão o maior ângulo entre a barra e a vertical seja ?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Nessa questão, temos uma partícula que bate horizontalmente numa barra. Inicialmente a barra está pendurada em repouso na vertical e depois da colisão, ela sofre uma rotação.
Na figura abaixo, podemos observar o diagrama que representa o sistema depois da colisão:
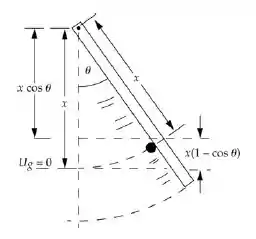
A questão quer a velocidade da partícula para gerar um .
Uma coisa muito últil que a gente pode usar em problemas de colisões são as equações de conservação. Então se lembra dessa dica!
Passo 2
Aplicando a conservação da energia mecânica, temos:
Vamos considerar que a nossa origem seja na altura inicial da partícula, então podemos dizer que a energial potencial é nula no começo do movimento.
E quando , o movimento vai terminar porque a velocidade do sistema vai ser zero. Então a energia cinética final é nula.
Então a equação de conservação da energia fica assim:
Substituindo as fórmulas pra energia cinética e potencial:
Passo 3
Aplicando conservação de quantidade de movimento angular, temos:
Sabemos que:
Logo:
Substituindo na equação da energia mecância temos:
Passo 4
Simplificando, temos:
Aplicando para , temos: