Tipler – Volume 1 – 6ª Ed. - Capítulo 9 – Seção 1 – Questão 64
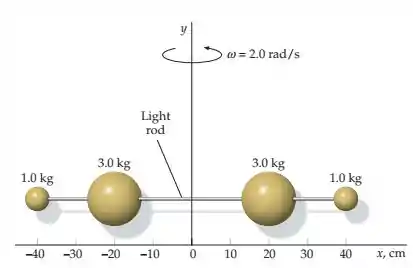
(Capítulo 9.1 – Exercício 64) As partículas da figura estão ligadas por uma barra muito leve. Elas giram em torno do eixo a . (a) Determine a rapidez de cada partícula e utilize esses valores para calcular a energia cinética do sistema diretamente a partir de . (b) Determine o momento de inérica em relação ao eixo , calcule a energia cinética a partir de e compare seu resultado com o resultado da parte (a).
Passo 1
E aí gente, belezinha?
Nessas questões de rotação, o que a gente não pode esquecer de jeito nenhum é que se as coisas estão ligadas por uma mesma barra, elas têm a mesma velocidade angular, e o que vai ser diferente são as velocidades, que a gente vai relacionar por
Então vamos lá!
Passo 2
Passo 3
a) Para as massas de 3,0kg:
Como são duas iguais, a energia dessas massas vai ser o dobro da de uma só:
Para as massas de 1,0kg, a operação vai ser igualzinha:
Logo, a energia total do sistema vai ser igual à soma das energias das massas:
Passo 4
b) Aqui é só a gente usar a definição de momento de inércia! De novo, as massas iguais vão ter momentos de inércia iguais.
A energia cinética em função do momento de inércia é:
Deu igualzinho à letra A. Ainda bem, senão ia dar bug na matrix!