Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Não-Ideais

Ver Teoria
Exercício 2012345678910111213141516171819212223242526272829303132333435363738394041424344454647

Enunciado

Tipler – Volume 1 – 6ª Ed. - Capítulo 9 – Seção 1 – Questão 76

(Capítulo 9.1 – Exercício 76) O sistema da figura 9-57 é largado do repouso quando o bloco de 30 k g está 2,0 m acima da prateleira. A polia é um disco uniforme de 5,0 k g com um raio de 10 c m . Justo antes de o bloco de 30 k g   atingir a prateleira, determine (a) sua rapidez, (b) a rapidez angular da polia e (c) a tensão nos fios. (d) Determine o tempo de queda do bloco de 30 k g . Suponha que o fio não deslize na polia.

Passo 1

Salve salveeeee, tudo certinho?

Vamos com calma que essa é bem grande. Nesse tipo de questão é bom usar conservação de energia para poder mexer com as velocidades, fechou?

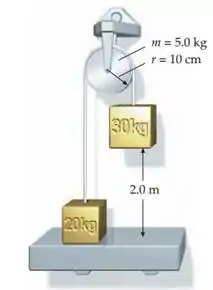
Então vamos lá!

Passo 2

a) Então vamos! Conservando a energia:

M g h = m g h + M v 2 2 + m v 2 2 + 1 2 I ω 2

30 × 9,81 × 2 = 20 × 9,81 × 2 + 20 v 2 2 + 30 v 2 2 + I ω 2 2

392,4 = 50 v 2 + I ω 2

Como a gente sabe, o momento de inércia da polia é I = 1 2 M p R 2 e na rotação, v = ω r .

50 v 2 + 1 2 M p R 2 v R 2 = 392,4

50 v 2 + 1 2 × 5 v 2 = 392,4

v 2 = 784,8 105

v = 2.73 m s

Passo 3

Passo 4

b) Aqui basta a gente relacionar a velocidade escalar e a angular, assim:

v = ω R

Substituindo os valres:

2.73 = ω × 0.1

ω = 27.3 r a d s

Passo 5

c) Agora vamos brincar de dinâmica. Usando a segunda lei de Newton para os blocos:

T 1 - m g = m a → T 1 = 20 ( a + g )

M g - T 2 = M a → T 2 = 30 ( g - a )

Como sabemos a velocidade e altura, podemos encontrar a aceleração pela equação de Torricelli!

v 2 = v 0 2 + 2 a h

2.73 2 = 2 a × 2

a = 1.87 m s 2

Substituindo nas trações:

T 1 = 20 1.87 + 9.81 → T 1 = 0.230 k N

T 2 = 30 9.81 - 1.87 → T 2 = 0.240 k N

Passo 6

d) Agora, pra achar o tempo, é só a gente analisar o movimento acelerado do bloco.

h = a t 2 2

Isolando t :

t = 2 h a

Substituindo os valores:

t = 2 × 2 1.87

t = 1.5 s

Ufaaa, acabou!!

Resposta

  1. v = 2.73 m s
  2. ω = 27.3 r a d s
  3. T 1 = 0.230 k N , T 2 = 0.240 k N
  4. t = 1.5 s

Exercícios de Livros Relacionados

Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,