UNICAMP, Sem Campus, Física 2, Listas de Física 2 - UNICAMP - Lista 1 - Gravitação, Questão 6
Qual é o módulo e qual é a direção da força gravitacional resultante sobre a massa de da figura ?
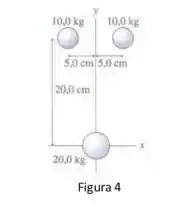
Passo 1
Eaew, belezinha?
Bem… o enunciado poupou palavras nessa! Mas, o esquema é o seguinte
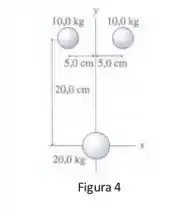
temos que calcular a força gravitacional sobre a partícula de massa que está na parte inferior da figura . Como fazemos isso? Usando a lei da gravitação universal de Newton, que tem a seguinte forma
em que é a distância entre duas partículas de massa e e a é a direção deste vetor! Bora tentar aplicar essa fórmula! Saca só!
Passo 2
Vamos montar aqui um diagrama de forças, temos que
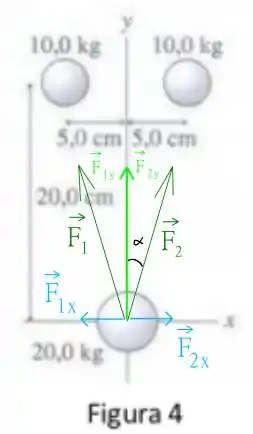
como temos que as duas partículas acima tem a mesma massa , temos que
já que temos uma simetria no problema que indica que . Isso é bom, pois essa simetria nos garante que as componentes em das forças se eliminam (veja figura, elas apontam em direções contrárias), e as forças em se somam, de forma que a nossa força resultante é
Vamos tentar encontrar a força explicitamente! Vem comigo!
Passo 3
Primeiro, temos que as componentes em , obedecem a seguinte relação
O cosseno pode ser obtido fazendo
temos que o cateto adjacente é a altura que as partículas estão, ou seja,
e, a hipotenusa pode ser obtida através do teorema de pitágora como
ou simplesmente . Portanto, o nosso cosseno será
e, a componente da força será
Vamos agora calcular a força usando a lei de gravitação universal de Newton!
Passo 4
Pela lei de gravitação universal de NEwton temos que
Temos então que nossa força resultante será
substituindo , e , assim como , temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!