UNICAMP, Sem Campus, Física 2, Listas de Física 2 - UNICAMP - Lista 1 - Gravitação, Questão 1b
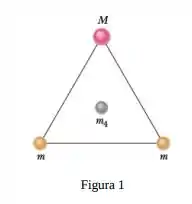
Como mostra a figura , duas esferas de massa e uma terceira esfera de massa formam um triângulo equilátero e uma quarta esfera de massa ocupa o centro do triângulo. A força gravitacional sobre a esfera central é nula.
Se dobrarmos o valor de , qual será o novo módulo da força gravitacional a que está submetida a esfera central?
Passo 1
Eaew, belezinha contigo?
A figura resume o esquema descrito no enunciado
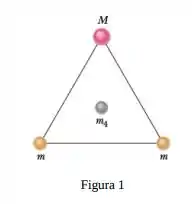
A alternativa pede para analisarmos qual será a nova força resultante sobre a partícula central se a massa dela se tornar . Vamos usar a a gravitação universal de Newton para obter uma fórmula para a nossa força resultante! Saca só!
Passo 2
Usando o diagrama de forças que usamos na alternativa anterior, nós tínhamos obtido as seguintes equações
e, na direção
usando as relações trigonométricas que apresentei na alternativa anterior, temos que
e, como
temos que
nós também obtivemos que
Portanto, temos que
e, portanto, as equações são tal que
e
Bora escrever explicitamente agora! Saca só!
Passo 3
Pela lei da gravitação universal, temos que
Note que e que , portanto, temos que
e
ou seja, a primeira equação é sempre independente do valor de . Mas a componente em , depende do valor de , saca só
note que a condição de equilíbrio não muda tendo em vista o valor de , mas, a resultante será tal que
se usarmos . A questão foi essa! Te vejo na próxima! Tchau Tchau!