UNICAMP, Sem Campus, Física 2, Listas de Física 2 - UNICAMP - Lista 1 - Gravitação, Questão 5a
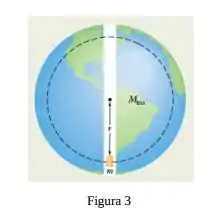
Suponha que um planeta é uma esfera homogênea de raio que (de alguma forma) possui um túnel radial estreito que passa pelo centro do planeta (figura 3). Suponha também que é possível posicionar uma maçã em qualquer lugar do túnel ou do lado de fora do planeta. Seja o módulo da força gravitacional experimentada pela maçã quando está na superfície do planeta. A que distância da superfície está o ponto no qual o módulo da força gravitacional que o planeta exerce sobre a maçã é se a maçã for deslocada:
Para longe do planeta?
Passo 1
Oiie, tudo bem com você?
A situação que temos é dada pela seguinte figura
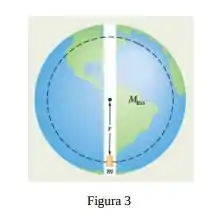
o fato do corte ser estreito quer dizer que não precisamos considerar variações no raio da esfera (Terra) devido ao corte. O enunciado pede para avaliarmos duas situações (uma para cada alternativa), a primeira alternativa requer que encontremos a distância do centro tal que a força gravitacional seja dada por
em que é o módulo da força gravitacional na superfície da esfera, e é a força gravitacional a uma distância qualquer . Vamos usar a lei da gravitação universal de Newton e o teorema das cascas para tentar resolver esse problema!
Passo 2
A lei da gravitação universal de Newton diz que o módulo da força gravitacional é dada por
o que tem validade em nosso problema, pois, pelo teorema das cascas, uma esfera de massa exerce uma força gravitacional sobre uma partícula de massa , como se toda a sua massa estivesse no centro. Agora, queremos que
Podemos então obter a distância do centro de nossa esfera como
ou simplesmente
A distância a partir da superfície, será dada então por
A primeira alternativa foi isso! Te vejo na próxima!