UNICAMP, Sem Campus, Física 2, Listas de Física 2 - UNICAMP - Lista 1 - Gravitação, Questão 3
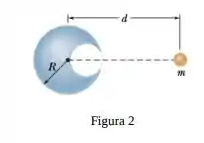
A figura mostra uma cavidade esférica no interior de uma esfera de chumbo de raio ; a superfície da cavidade passa pelo centro da esfera e “toca” o lado direito da esfera. A massa da esfera antes de ser criada a cavidade era . Com que força gravitacional a esfera de chumbo com a cavidade atrai uma pequena esfera de massa que se encontra a uma distância do centro da esfera de chumbo, sobre a reta que liga os centros das esferas e o centro da cavidade?
Passo 1
Eaew, tudo certinho?
Esse é um problema clássico! Temos uma esfera de raio com uma cavidade, esse objeto exerce uma força gravitacional sobre uma partícula de massa . Originalmente, a nossa esfera tinha uma massa , e a partícula está a uma distância . O esquema é o seguinte
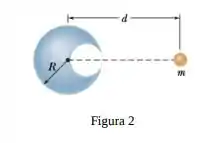
Okay, mas e como calculamos essa força gravitacional? O segredo aqui está em usar o Teorema das Cascas para a gravitação e o teorema da superposição! Saca só!
Passo 2
Se tivéssemos uma esfera cheia de raio , o teorema das cascas diz que poderíamos tratar essa esfera como uma partícula de massa , portanto, a força gravitacional seria a força gravitacional entre duas partículas, dada por
Mas, não temos uma esfera cheia! De nossa esfera cheia foi arrancada uma outra esfera. Quanta força gravitacional era relativa a essa esfera retirada? Considerando que arrancamos uma esfera de raio , a distância do centro da cavidade até a partícula é dada por , e portanto, a força gravitacional é dada por
O princípio da superposição, nos garante então que, a força gravitacional total será dada por
Note que tive que subtrair o valor, pois em nosso problema, a cavidade é uma esfera que foi removida, portanto, a força gravitacional que ela faria, ela não faz mais! Ainda precisamos encontrar a massa , bora lá!
Passo 3
Se essa é uma esfera uniforme, temos que a massa é igualmente distribuída pela esfera, portanto, temos que
em que é a densidade da esfera. Usando que o volume da cavidade é dado por
e, como o volume da esfera original é , temos que a massa da cavidade por ser obtida como
Vamos usar isso em nossa força gravitacional!
Passo 4
Usando as massas que obtivemos, temos que
Ótimo! Agora podemos substituir valores, temos que
calculando alguns produtos, temos que
ou simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!