UNICAMP, Sem Campus, Física 2, Listas de Física 2 - UNICAMP - Lista 1 - Gravitação, Questão 2
Três estrelas, cada uma com a massa do Sol, formam um triângulo equilátero com lados de . (Este triângulo se encaixaria com precisão da órbita de Júpiter). O triângulo precisa girar, pois do contrário, as estrelas colidiram no centro. Qual é o período de rotação? Expresse sua resposta em anos.
Passo 1
Oiie, tudo bem?
Vou desenhar um esqueminha que descreve o nosso problema, temos o seguinte triângulo equilátero
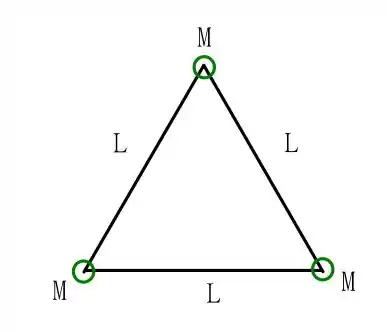
em que , a massa do Sol, e os lados são dados por . Queremos achar o período de rotação deste sistema. Para isso, vamos estudar a força centrípeta resultante que causa a rotação destas massas em torno do centro do triângulo, e ver qual velocidade angular iremos obter, uma vez que
vale a pena relembrar a lei da gravitação universal de Newton como
em que Bora lá!
Passo 2
Vamos escrever o diagrama de forças relativo a uma das partículas (todas elas vão estar rotacionando juntas, então não importa qual você escolher), temos que
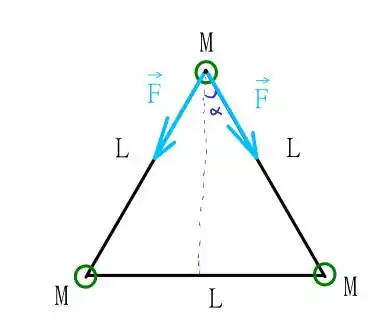
Note que as componentes verticais darão a nossa força centrípeta e as componentes horizontais irão se eliminar, uma vez que temos o seguinte esquema para elas
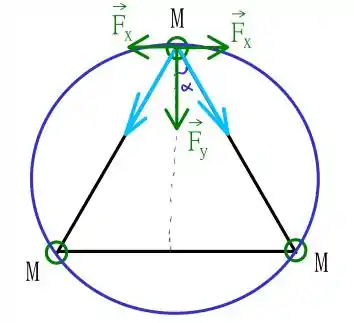
Note que abusei um pouco da notação no esquema acima! Mas o que importa é que temos duas forças iguais se somando apontando para o centro da órbita, e duas forças iguais se subtraindo tangenciais a órbita a todo instante de tempo. A componente vertical é dada por
em que podemos usar a lei da gravitação de Newton para obter que
e, a componente , será dada por
Vamos precisar achar esse ângulo! Vem comigo!
Passo 3
Podemos usar o triângulo retângulo de hipotenusa , e catetos e , para escrever que
mas quanto vale Usando pitágoras, temos que
e, desta maneira, obtemos
ou seja, temos que
sendo assim a componente vertical de nossa força é
e, portanto,a força centrípeta resultante, será dada por
Vamos usar isso para encontrar a nossa velocidade angular! Saca só!
Passo 4
A força centrípeta pode ser identificada como
em que é o raio da circunferência. Em nosso caso, como nossa órbita passa pelos vértices do triângulo, o centro da órbita é o centro do triângulo equilátero, desta maneira, vamos precisar relembrar que o centro do triângulo equilátero, é relacionado com a sua altura, temos que o segmento de reta que liga a partícula considerada ao centro do triângulo tem comprimento dado por
Se não entender essa parte, dê uma revisada em como encontrar as coordenadas do baricentro de um triângulo equilátero, belezinha? Como achamos anteriormente que , obtemos que
De forma que a nossa expressão para a força centrípeta se torna
usando que a velocidade linear se relaciona com a velocidade angular por , usando o obtido, temos que
Maravilha! Vamos juntar os nossos resultados agora!
Passo 5
Usando a expressão para a força centrípeta que achamos antes, podemos pegar o seu módulo, para escrever que
se isolarmos a velocidade angular, temos que
vamos substituir as constantes do problema, para obter que
ou seja, o período será dado por
que equivale à
A questão é isso! Te vejo na próxima! Tchau Tchau!