UNICAMP, Sem Campus, Física 2, Listas de Física 2 - UNICAMP - Lista 1 - Gravitação, Questão 1a
Como mostra a figura , duas esferas de massa e uma terceira esfera de massa formam um triângulo equilátero e uma quarta esfera de massa ocupa o centro do triângulo. A força gravitacional sobre a esfera central é nula.
Qual é o valor de em termos de ?
Passo 1
Eaew, belezinha contigo?
A figura resume o esquema descrito no enunciado
a alternativa pede para que encontremos a massa , tal que a força gravitacional sobre a partícula no centro, de massa , sofra uma força resultante nula. Portanto, vamos usar a condição
em que, as forças em consideração podem ser obtidas pela lei da gravitação universal de Newton
em que é uma constante, e é o vetor que liga duas partículas quaisquer com direção dada por . Vamos tentar resolver isso agora! Bora lá!
Passo 2
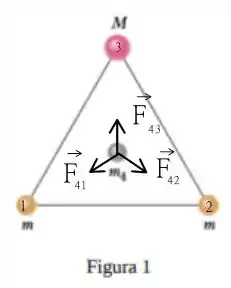
Primeiro, vamos escrever o diagrama de forças indicando as forças atuando sobre a partícula central, temos que
o referencial é escolhido tal que
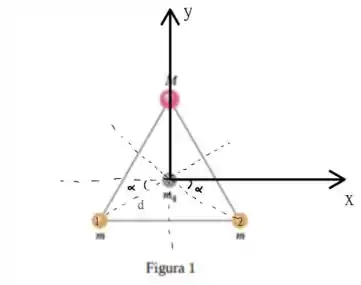
de forma que podemos escrever todos os vetores distância como , em que . Os ângulos serão importantes para fazermos as somas dos componentes de nossas forças! Saca só!
Temos que na direção as seguintes forças
e, na direção
da equação temos que , e, portanto, a equação nos retorna que
Ainda precisamos encontrar esse ângulo , mas para isso, vamos precisar lembrar algumas propriedades geométricas do triângulo equilátero. Saca Só!
Passo 3
A nossa partícula está no baricentro, então podemos dizer que
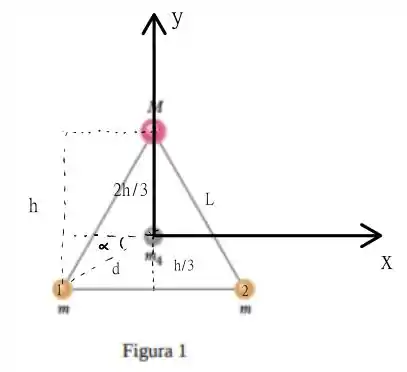
Usando pitágoras, temos que a altura é tal que
de forma que temos que
lembrando que
temos que o ângulo é obtido como
Mas note que
de forma que nosso ângulo é dado por
Vamos ver se isso é o suficiente para identificarmos a nossa massa! Saca só!
Passo 4
Usando a lei da gravitação universal de Newton, temos que a relação se torna
em que utilizei o resultado do passo anterior! Podemos isolar a nossa massa como
o que faz sentido certo? Se todas as massa são iguais, então a partícula no centro irá sofrer uma resultante nula! A primeira alternativa foi isso! Te vejo na próxima! Tchau Tchau!