Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
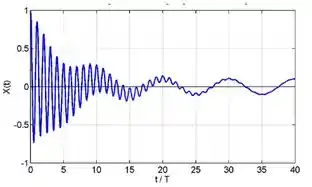
Na figura abaixo, os períodos dos regimes transitório e estacionário são:
- e
- e
- e
- e
- e
Passo 1
A primeira coisa que precisamos perceber nessa questão é quando acaba o regime transitório e quando começa o regime permanente.
Como vimos no capítulo, no regime permanente o sistema oscila com amplitude constante. Assim, olhando o gráfico, dá pra ver que isso acontece após
Passo 2
Agora precisamos só contar o período dos dois regimes.
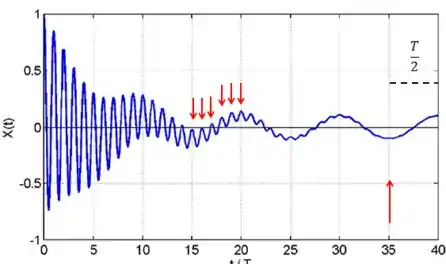
Para o regime transitório, podemos notar o intervalo de tempo que vai de até e perceber que ali existem 6 picos. Logo, existem intervalos de período.
Além disso, podemos notar também que após o a oscilação percorre meio período, até .
Dá uma olhada na figura:
Passo 3
Bora calcular o período do regime transiente então:
A diferença de tempo entre é dada por:
Como são 5 períodos ali:
Passo 4
E para o regime permanente:
A diferença de tempo entre e é:
Só que esse intervalo corresponde a meio período, assim:
E conseguimos (:
Resposta
a)