Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Dois sistemas massa mola encontram-se acoplados como mostra a figura. Sendo e a chamada razão áurea, o sistema tem dois modos normais com frequências e tais que:
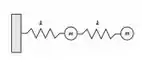
Observação: Existe um erro no enunciado: . O correto é . Além disso, não encontramos uma resposta que esteja listada acima.
Passo 1
Primeiramente, vamos determinar as forças que agem em cada bolinha.
Para a nossa análise, vamos considerar que a bolinha mais próxima da parede tem um deslocamento , positivo, e a outra bolinha tem um deslocamento também positivo:
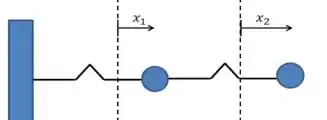
Com isso, as forças que agem em cada bolinha são representadas abaixo:
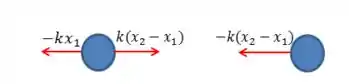
Passo 2
Aplicando a segunda lei de Newton pra cada bolinha:
E obtivemos o sistema de EDO’s acima. Beleza?
Passo 3
Agora vamos usar a dica do enunciado. Vamos supor que as soluções das equações sejam:
Substituindo nas equações:
Lembrando que:
Assim:
Isolando nas duas equações:
Como não estamos interessados na solução trivial( devemos ter:
Passo 4
Voltando ao sistema:
Podemos escrevê-lo como o produto vetor matriz abaixo:
Como não queremos uma solução trivial o determinante da matriz maior tem que ser nulo.
Assim:
Passo 5
Agora devemos resolver a equação biquadrada acima. Lembra como faz? Só a gente considerar e Assim:
Calculando o
Assim:
Isso tudo igual a:
NOTA: o enunciado está errado. Ele chama , quando na verdade é
Então as frequências dos modos normais são:
Observe que também teríamos as frequências:
E:
Já que se:
Porém, as frequências devem ser positivas, certo? Já que elas são dadas por:
E :
Sempre! Assim, devemos descartar essas opções negativas.
Passo 6
Com isso, não achamos uma resposta correspondente no gabarito. Acreditamos que existem erros no enunciado.
Resposta
Sem resposta no gabarito. Frequências dos modos normais achadas: