Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Considere um oscilador amortecido e sujeito a uma força cossenoidal. As condições iniciais do oscilador podem
- Ampliar ou reduzir a amplitude nos instantes iniciais do movimento.
- Influenciam a amplitude do movimento mesmo em instantes muito posteriores ao início do movimento.
- Não têm qualquer influência sobre o movimento.
- Só podem aumentar a amplitude no início, pois o amortecimento reduzirá a amplitude de oscilação até o oscilador parar completamente.
- Só podem aumentar a amplitude no início, pois o amortecimento reduzirá a amplitude de oscilação até um valor constante não nulo.
Passo 1
Essa questão testa os seus conhecimentos sobre regime transitório, regime permanente e ressonância.
Passo 2
Vamos recapitular um pouco da nossa teoria: Se um sistema oscila sujeito a uma força externa, decorrido um certo tempo, ele passará a oscilar com a frequência dessa força externa. Além disso, ele passará a oscilar com uma amplitude que é função da força externa. Matematicamente:
E antes disso? Antes disso, a solução tem um regime transitório. Nesse regime, a solução é dada por:
Onde é a solução da equação homogênea. Essa equação que depende das condições iniciais do problema.
Então qual é a conclusão? Com o tempo, essa solução homogênea desaparece.
Como só ela depende das condições iniciais, a solução do sistema após um longo tempo não depende das condições iniciais.
Passo 3
Como vimos no capítulo, um gráfico típico pra esse sistema é esse aqui:
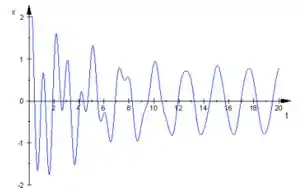
Como você pode ver, no inicio a amplitude pode aumentar e diminuir, mas depois de um certo tempo ela fica estável.
Com tudo isso, podemos dizer que a solução correta é a:
Resposta
a)