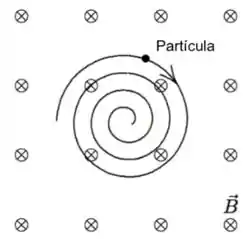
Um campo magnético uniforme e estacionário aponta para dentro do plano da página. Uma partícula carregada, movendo-se no plano da página, segue uma espiral no sentido horário de raio decrescente, como mostrado na figura abaixo. Uma explicação razoável para esta trajetória é:
- A carga da partícula é positiva e sua velocidade está diminuindo.
- A carga da partícula é positiva e sua velocidade está aumentando.
- A carga da partícula é negativa e sua velocidade está aumentando.
- A carga da partícula é negativa e sua velocidade está diminuindo.
- Não há dados suficientes para dar uma explicação razoável.
Passo 1
Bom, nessa questão temos uma partícula carregada que faz um movimento circular na presença de um campo magnético. O que a gente precisa se ligar nesse tipo de questão é que a força centrípeta nesse movimento vai ser a própria força magnética e o raio dessa trajetória circular é dado por:
(o famoso Rabib, Me Vê um QuiBe rs)Então, temos que avaliar nessa questão 2 fatores.
1º se a carga dessa partícula é positiva ou negativa e para isso vamos ter que pensar em regra da mão direita
2º A velocidade dessa partícula aumenta ou diminui e para isso vamos olhar para a fórmula do raio da trajetória circular. Bora lá?
Passo 2
A força magnética é dada pela expressão:
Portanto, a direção dessa força é dada pelo produto vetorial da velocidade com o campo magnético. Fazendo a regra da mão direita, você deve colocar os 4 dedos da sua mão direita na direção da velocidade da partícula e a palma da mão na direção com campo magnético, fazendo isso, seu polegar apontará na direção da força magnética.Fazendo isso, teremos o seguinte:
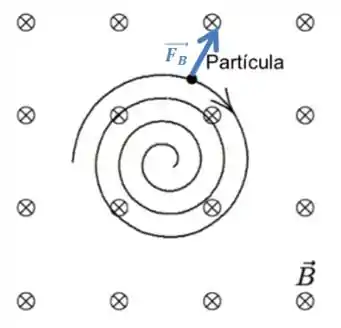
Esse é o sentido da força magnética caso a partícula tivesse uma carga positiva. No entanto, para realizar um movimento circular, a força magnética deve apontar para o centro do movimento (e nesse caso ela estaria apontando para fora).
No caso da partícula ter uma carga negativa, a força magnética tem sentido oposto ao que encontramos na regra da mão direita, e nesse caso, teríamos a força magnética apontando para o centro do movimento, que é o esperado
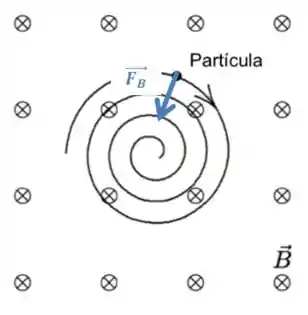
Portanto, a carga é negativa.
Passo 3
Agora, só nos resta avaliar se a velocidade deve aumentar ou diminuir. Olhando para a trajetória dessa partícula, percebemos que o raio dela diminui com o tempo, certo?
E sabemos que o raio dessa trajetória circular é dado por:
Percebe que o raio tem uma relação diretamente proporcional com a velocidade? Isso é, se a velocidade aumenta, o raio aumenta e se a velocidade diminui o raio também diminui.Portanto, como o raio dessa trajetória vai diminuindo, a velocidade diminui também.
A resposta é a letra d).
Resposta
Letra d).