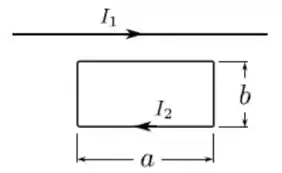
Considere uma espira retangular de lados e () e um fio retilíneo infinito, no mesmo plano da espira. Sabendo que o fio retilíneo é paralelo aos lados longos da espira e que o fio e a espira portam, respectivamente, correntes estacionárias para a direita e no sentido horário, assinale a única opção INCORRETA.

1. A força sobre cada um dos lados curtos da espira é não-nula.
2. A soma vetorial das forças sobre os lados curtos da espira é nula.
3. A soma vetorial das forças sobre os lados longos da espira é nula.
4. As forças sobre os lados longos da espira estão na mesma direção.
5. A força resultante sobre a espira tem direção perpendicular ao fio retilíneo.

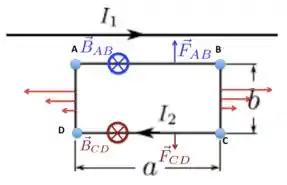
No caso do nosso problema aqui, como a corrente está passando no fio da esquerda para a direita, então o campo magnético estará entrando no plano da página e, por isso, perpendicular a todos os lados da espira.

No lado , o campo magnético   é mais intenso, porque está mais próximo do fio e como a força sobre um condutor transportando corrente é dada por

no lado da espira a força  será mais intensa e apontando para cima, como mostra a figura.

No lado , a força   terá a mesma direção de  , mas será menos intensa, pois está a uma distância maior do fio com corrente , e está apontando para baixo, como também é desenhado na figura acima.

A força sobre cada um dos lados mais curtos da espira é diferente de zero e varia ao longo do comprimento, pois o valor do campo magnético é diferente em cada um dos pontos desses lados.

No entanto, as forças sobre um desses lados têm a mesma direção, mesma intensidade, porém sentidos contrários que as outras forças do lado mais curto oposto, como a gente colocou em vermelho lá na figura. Portanto, em cada um dos lados mais curtos existe uma força resultante, mas a soma vetorial das forças sobre os DOIS FIOS é nula.

Agora, se a gente olha para a força resultante sobre TODA A ESPIRA, percebemos que existirá uma força resultante que estará perpendicular aos fios e , pois as  e  têm intensidades diferentes.