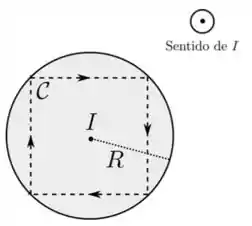
Um fio condutor retilíneo tem seção transversal circular de raio , como mostrado na figura abaixo. Uma corrente estacionária de intensidade atravessa o fio com sentido para fora do plano do papel, uniformemente distribuída sobre a seção transversal. Desenha-se então uma curva fechada e orientada na forma de um quadrado inscrito no perímetro dessa seção, com a orientação indicada. Nessa situação, podemos afirmar que a circulação do campo magnético produzido pelo fio ao longo de , dada por , vale:
Passo 1
A primeira coisa de que precisamos nos lembrar é que a circulação do campo magnético é dada por
em que é a corrente que passa através da área definida pela curva fechada . No caso desta questão, essa área é um quadrado e é dada por .
Como a corrente é uniformemente distribuída, significa que a densidade de corrente é a mesma através da seção transversal circular de raio e através da área do quadrado de lado , ou seja,
de onde a gente tira que
Ainda não conhecemos o valor de !!
Passo 2
Da figura, vemos que o diâmetro do círculo é igual a . Portanto,
Dessa expressão, tiramos que o lado do quadrado é
Substituindo na expressão para , temos
Passo 3
Resta, agora, vermos qual é o sinal da circulação. Bom, como a corrente está saindo do plano da página, então, pela regra da mão direita, a gente aponta o polegar no sentido da corrente e gira os dedos em torno do polegar. Esse sentido será o anti-horário e, portanto, será o sentido positivo.
Como a curva fechada está no horário, ou seja, contrário ao sentido dado pela regra da mão direita, então devemos ter uma circulação negativa, isto é,
Resposta
Letra a).