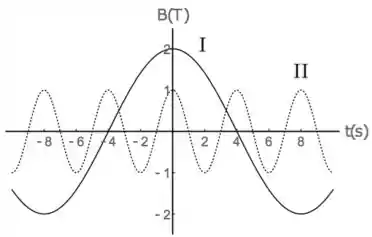
Considere duas situações: na primeira, uma espira circular de área é atravessada perpendicularmente por um campo magnético uniforme que oscila periodicamente no tempo de acordo com a curva na figura abaixo (curva cheia), e na segunda situação, a mesma espira é atravessada perpendicularmente por um campo magnético uniforme oscilante descrito pela curva (pontilhada). Podemos afirmar que a maior amplitude do fluxo de campo magnético e a maior amplitude da fem induzida ocorrem, respectivamente, nas situações
- Não é possível determinar sem conhecer a resistência elétrica da espira.
Passo 1
A primeira coisa que precisamos entender nesta questão é como são os campos magnéticos de cada caso. Olhando para a figura, vemos que a forma geral desses campos é
em que é a amplitude do campo, , com sendo o período, e a fase inicial desse campo.
Para ambas as curvas, a fase inicial é zero, ou seja, temos . Tendo isso e olhando para a figura, conseguimos escrever a expressão para cada campo, já que a figura mostra os valores máximos para cada caso. Portanto,
em que esse que aparece é a unidade para o campo magnético.
Beleza?
Passo 2
Mas a figura também mostra algo a mais sobre esses campos. Dá uma olhada lá e veja que o campo e que Olhando para esse instante de tempo , vemos que os períodos das curvas têm a seguinte relação:
Simplificando essa expressão, temos .
Passo 3
Agora, vamos olhar para os fluxos magnéticos de cada caso. Como o campo magnético é uniforme e é sempre perpendicular à área, os fluxos magnéticos em cada caso serão dados pelas seguintes expressões:
Como os campos magnéticos oscilam no tempo e a amplitude de oscilação do campo é maior, temos que as amplitudes são tais que:
em que o nessas relações faz referência à unidade de medida .
Passo 4
Por último, o módulo da fem induzida dependerá da derivada do campo magnético. Como derivada de seno e cosseno também resulta em funções seno e cosseno, as fems’s induzidas também oscilarão. Então, basta considerarmos as amplitudes dessas fem’s.
Portanto, para o caso da curva , depois de derivar com relação ao tempo, encontramos a amplitude
Para a curva , teremos
Resumindo:
e
Resposta
Letra c).