UFRJ- Física 3 – PF 2018.1 - DIURNO - 14
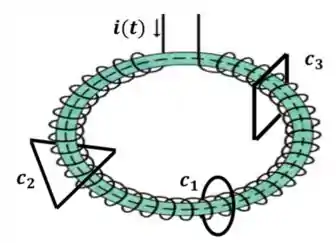
Considere um solenóide toroidal de seção transversal de raio . Ele é atravessado por uma corrente de intensidade que varia lentamente com o tempo. Considere também três espiras orientadas paralelamente às seções transversais do solenoide: , uma espira circular de raio , , uma espira triangular de lados iguais a e , uma espira quadrada de lado , dispostas no solenóide como mostrado na figura abaixo, envoltas e centralizadas no mesmo. Sejam , e as indutâncias mútuas entre o solenóide e as espiras , e , respectivamente, quando consideradas individualmente. Nessa situação, podemos afirmar que:
Passo 1
A indutância mútua é dada por
em que é o fluxo total através de cada uma das espiras.
O fluxo, como a gente já viu, depende tanto do campo magnético quando da área através da qual esse campo magnético passa.
Agora vem o grande detalhe desta questão. Apesar de as geometrias de cada espira serem diferentes, o mesmo campo magnético produzido pela corrente atravessa a mesma área circular de todas as espiras , e e só tem campo magnético nessa região circular de cada uma das espiras.
Em outras palavras, de toda a área de cada espira, apenas uma área circular igual à seção transversal do toróide é que tem campo magnético e que vai ser atravessada por esse campo magnético, que está dentro da região verde do toróide.
Por isso, se o fluxo total é o mesmo através de cada uma das espiras e a corrente produzindo o campo que atravessa as espiras também tem o mesmo valor, temos o seguinte:
Resposta
Letra g).