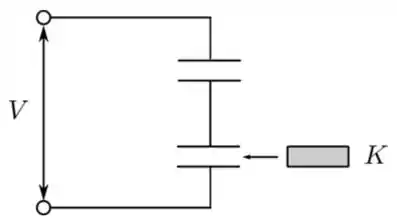
Dois capacitores idênticos, inicialmente no vácuo, são conectados aos terminais de uma bateria que fornece uma diferença de potencial constante , como mostrado na figura abaixo. A seguir, mantendo a bateria conectada, insere-se uma placa isolante de constante dielétrica entre as placas de um dos capacitores, de forma a ocupar todo o volume entre elas. Nessa situação, é correto afirmar que, após a inserção:
- A carga armazenada no capacitor com o dielétrico diminui com relação ao valor original.
- Os dois capacitores armazenam a mesma energia.
- A carga armazenada no capacitor que permanece no vácuo aumenta com relação ao valor original.
- Os dois capacitores terão a mesma diferença de potencial entre suas placas.
- A energia armazenada no capacitor que permanece no vácuo diminui com relação ao valor original.
Passo 1
Primeiro vamos entender o que está acontecendo
Quando o dielétrico é colocado no capacitor debaixo a sua capacitância aumenta para
Onde é a constante dielétrica do material.
A capacitância equivalente do sistema irá mudar também! Como os dois capacitores estão em série vamos ter
Como as duas capacitâncias estão sempre em contato com a bateria então a carga nos capacitores vai aumentar, ou seja
Pra poder comparar temos que calcular a carga antes de inserir o dielétrico, assim a capacitância equivalente antes de inserir o dielétrico será
E a carga antes de inserir o dielétrico será
Agora podemos comparar a carga antes e depois de inserir o dielétrico!
Como , então é maior que também, então , ou seja, ao adicionarmos o dielétrico no capacitor de baixo, a carga nos dois capacitores aumenta!
E a ddp? Bem temos que a soma delas tem que ser igual à ddp da bateria
Antes de inserir o dielétrico as ddps eram as mesmas e eram dadas por
Após inserir o dielétrico cada uma delas é dada por
Aqui vemos que a ddp do capacitor de cima aumentou!
Aqui vemos que a ddp do capacitor de baixo diminuiu!
Beleza! Agora vamos olhar cada um dos itens!
Passo 2
(a) A carga armazenada no capacitor com o dielétrico diminui com relação ao valor original.
Já discutimos que o valor da carga no capacitor com dielétrico tem que aumentar, então essa está errada.
Passo 3
(b) Os dois capacitores armazenam a mesma energia
Lembra como é a equação da energia armazenada num capacitor? É essa aqui ó:
Como esses capacitores estão em série então eles compartilham a mesma carga. Pra isso vale mais a pena a usar a expressão que tem e , usando
Então a energia armazenada no capacitor de cima será
E o de baixo
Ou seja, as energias armazenadas em cada um dos capacitores são diferentes entre si. Assim essa frase está errada também!
Passo 4
(c) A carga armazenada no capacitor que permanece no vácuo aumenta com relação ao valor original.
Já falamos que o capacitor de baixo vai ter a sua carga aumentada! Como o capacitor de cima está em série com o de baixo e capacitores em séries têm a mesma carga, a carga no capacitor de baixo também aumentará!
Então essa frase é verdadeira!
Vamos dar uma olhada nas outras pra garantir?
Passo 5
(d) Os dois capacitores terão a mesma diferença de potencial entre suas placas.
Quando temos capacitores em série o que acontece é que
Essa ddp se divide igualmente quando os capacitores têm a mesma capacitância, só que no nosso caso
Ou melhor dizendo
Ou seja, essas diferenças de potencial não são iguais entre si (apesar da soma entre elas ser sempre ).
Na verdade também fizemos a big conta no passo 1 mostrando que essas ddps são diferentes!
Essa frase está errada!
Passo 6
(e) A energia armazenada no capacitor que permanece no vácuo diminui com relação ao valor original.
A energia armazenada no capacitor de cima é dada por
Como a capacitância dele permaneceu a mesma basta olhar para sua ddp! Já discutimos no passo 1 que a sua ddp aumenta, então a energia armazenada nele também irá aumentar!
Logo essa afirmação está errada também!
Resposta
Letra c).