Achar a equação da hipérbole centrada na origem com focos nos pontos e e que passa pelo ponto .
Passo 1
Bora praticar mais sobre as hipérboles!! Queremos achar agora a equação da hipérbole que está centrada na origem, ou seja, , possui seus focos em e e passa pelo ponto . Para comerçar vamos fazer um esboço com os dados que temos.
Passo 2
Esboçando teremos:
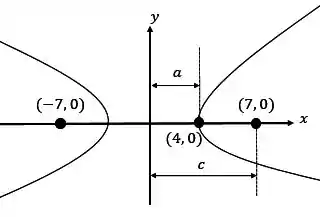
Então, sabemos que estamos no CASO 1. Pela figura, conseguimos descobrir o valor de e .
Com a relação :
Passo 3
Sabendo os valores de e e ainda sabemos da teoria que se estamos na CASO 1, a equação da hipérbole possui o seguinte jeitão:
Então, teremos:
Pronto!! Terminamos!!
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Centro C ( 2 , - 3 ) , eixo real paralelo a O y e passando por ( 3 , - 1 )
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Focos F 1 - 1 , - 5 eF 2 ( 5 , - 5 ) e que seja hipérbole equilátera.
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Vértices A 1 - 3 , - 4 e A 2 ( - 3,4 ) e que seja hipérbole equilátera.
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Centro C ( - 2,1 ) , eixo real paralelo a O x e passando por ( 0,2 ) e ( -
Em cada um dos problemas 38 a 43, determinar a equação reduzida, o centro, os vértices, os focos, a excentricidade e equações das assíntotas das hipérboles dadas. Esboçar o gráfico. 9 x 2 - 4 y 2 - 18