Determine as equações de todas as hipérboles que têm distância focal e cujas assíntotas são as retas .
Passo 1
Como as assíntotas se intersectam na origem e são simétricas em relação aos eixos, as hipérboles estarão em posição canônica, centradas na origem.
As assíntotas da hipérbole são e as assíntotas da hipérbole são .
Temos que e .
Para a primeira, temos que , daí temos que
Logo, essa hipérbole é
Para a segunda hipérbole,
Logo, essa segunda hipérbole é
Por fim, temos isso aqui
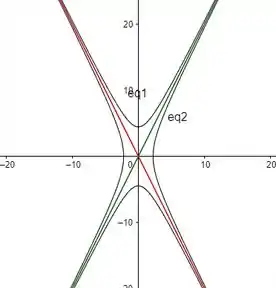
Onde a reta verde é e a reta vermelha é .
Resposta
e
Exercícios de Livros Relacionados
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Centro C ( 2 , - 3 ) , eixo real paralelo a O y e passando por ( 3 , - 1 )
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Focos F 1 - 1 , - 5 eF 2 ( 5 , - 5 ) e que seja hipérbole equilátera.
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Vértices A 1 - 3 , - 4 e A 2 ( - 3,4 ) e que seja hipérbole equilátera.
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Centro C ( - 2,1 ) , eixo real paralelo a O x e passando por ( 0,2 ) e ( -
Em cada um dos problemas 38 a 43, determinar a equação reduzida, o centro, os vértices, os focos, a excentricidade e equações das assíntotas das hipérboles dadas. Esboçar o gráfico. 9 x 2 - 4 y 2 - 18