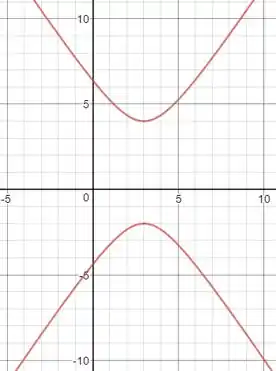
Determinar o centro, um esboço do gráfico, os vértices e os focos da hipérbole de equação:
Passo 1
Temos a expressão de um hipérbole e por meio dela devemos determinar: centro, vértices, focos e ainda fazer um esboço.
Vamos começar, então!!
Passo 2
Primeiro, devemos deixar a expressão parecida com uma das formas reduzidas que vimos na teoria!! Para isso, vamos completar quadrados e ajeitar a expressão:
Separando as coias que tem e
Podemos reescrever essa parte com da seguinte maneira
E vamos fazer a mesma coisa pra
Assim a nossa equação fica
Dividindo tudo por , temos:
Passo 3
Chegamos na forma do CASO 3. Com a expressão nesse formato conseguimos identificar o valor de e . O valor de continua a ser o maior valor do denominador, e o o menor, assim:
Para achar o valor de , usamos a relação :
Passo 4
Já temos os valores de e . Como estamos no CASO 3, vamos fazer uma mudança de coordenadas para então resolvermos o problema num sistema como se fosse o CASO 2. Assim, mudando as coordenadas por:
Nossa equação no sistema fica:
Pronto, agora estamos no CASO 2, e achamos os parâmetros normalmente.
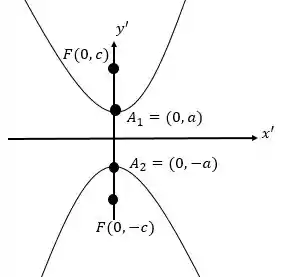
Nossa hipérbole estará como na figura acima no sistema , então teremos:
Substituindo os valores de e
Passo 5
Mas, cuidado, ainda não terminamos, pois esses valores que encontramos acima estão no sistema . Vamos voltar para o sistema usando as seguintes relações:
Pronto!! Agora sim achamos os parâmetros no . Só falta fazer o esboço!!
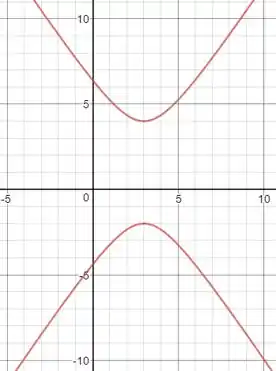
Resposta