Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Hipérboles

Ver Teoria
Exercício 612345789

Enunciado

UFPE – Geometria Analítica – 2019.1 – P2 – Questão 4

No plano R 2 , considere o ponto F = ( 0,5 ) e a reta l : y = 9 5 , mostre que o lugar geométrico C dos pontos X tais que d X , F = 5 3 d ( X , l ) é uma cônica.

  1. Identifique C .
  2. Determine os parâmetros geométricos de C .
  3. Determine a excentricidade de C .
  4. Faça um esboço de C .

Passo 1

  1. Pra determinar qual é a cônica, vamos abrir essa expressão que ele nos deu!

    2. d X , F = 5 3 d X , l

    O lado esquerdo é a distância de X a F , ou seja, de dois pontos. O lado direito é a distância de X a l , ou seja, de ponto a reta.

    x 2 + y - 5 2 = 5 3 y - 9 5

    Elevando os dois lados ao quadrado e desenvolvendo:

    x 2 + y 2 - 10 y + 25 = 25 9 y 2 - 18 5 y + 81 25

    9 x 2 + 9 y 2 - 90 y + 225 = 25 y 2 - 90 y + 81

    9 x 2 - 16 y 2 = - 144

    - x 2 16 + y 2 9 = 1

    - x 4 2 + y 3 2 = 1

    Essa é a equação de uma hipérbole!

    Passo 2

  2. Da equação que obtivemos no item (a), a gente sabe que:

    3. a = 3

    b = 4

    E da relação fundamental:

    c 2 = a 2 + b 2

    c = 3 2 + 4 2

    c = 5

    Portanto, os parâmetros geométricos são:

    Eixo transverso: 2 a = 6 ;

    Eixo conjugado: 2 b = 8 ;

    Distância focal: 2 c = 10 .

    Passo 3

  3. A excentricidade é moleza! É só usarmos a definição.

    4. e = c a = 5 3

    Passo 4

  4. Aqui vamos prestar atenção em algumas coisas: na equação da hipérbole,

- x 4 2 + y 3 2 = 1

O sinal positivo está no y , então esse é o eixo que corta os ramos da hipérbole. Temos que traçar as assíntotas. Na hipérbole, as assíntotas têm equação:

y = ± a b x = ± 3 4 x

Então, esboçando, vamos obter uma figura assim:

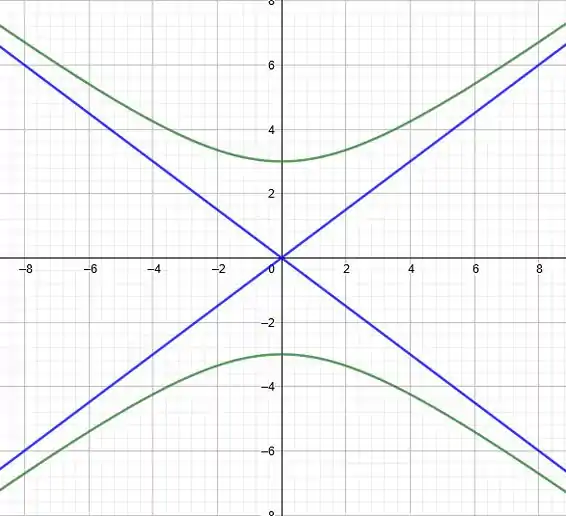
Resposta

  1. - x 4 2 + y 3 2 = 1 : hipérbole.
  2. Eixo transverso: 2 a = 6 ;

    3. Eixo conjugado: 2 b = 8 ;

    Distância focal: 2 c = 10 .

  3. e = 5 3

Exercícios de Livros Relacionados

Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Centro C ( 2 , - 3 ) , eixo real paralelo a O y e passando por ( 3 , - 1 )
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Focos F 1 - 1 , - 5 eF 2 ( 5 , - 5 ) e que seja hipérbole equilátera.
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Vértices A 1 - 3 , - 4 e A 2 ( - 3,4 ) e que seja hipérbole equilátera.
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Centro C ( - 2,1 ) , eixo real paralelo a O x e passando por ( 0,2 ) e ( -
Em cada um dos problemas 38 a 43, determinar a equação reduzida, o centro, os vértices, os focos, a excentricidade e equações das assíntotas das hipérboles dadas. Esboçar o gráfico. 9 x 2 - 4 y 2 - 18