Seja o lugar geométrica dos pontos do plano cujas coordenadas e satisfazem
- Qual o tipo da cônica ? Escrever a equação canônica de .
- Encontrar os focos, os vértices e a excentricidade de . No caso de hipérbole, encontrar também as equações das assíntotas no sistema .
Passo 1
Temos uma expressão que é a expressão de alguma das três cônicas que vimos: parábola, elipse ou hipérbole. No primeiro item devemos identificar a cônica e escrever a equação na forma canônica( ou reduzida). Já no segundo item devemos encontrar todos os elementos da cônica, como fizemos nos exercícios anteriores.
Passo 2
a) Para identificarmos a cônica vamos completar quadrados e ver com qual cônica expressão se assemelha.
Dividindo tudo por :
Bom, analisando a equação temos uma hipérbole!!
Para deixar a expressão numa forma reduzida, vamos fazer uma mudança de coordenadas de tal forma, que:
Então, teremos:
Item está feito!!
Passo 3
b) Focos, vértices, excentricidade e como é uma hipérbole, as assíntotas!!
Como podemos notar do item estamos no CASO 3, ou seja, na translação. Como já fizemos uma mudança de coordenadas para o sistema vamos achar os parâmetros nesse sistema como no CASO 1 e depois passamos para o sistema .
Da expressão , tiramos os valores de e .
O valor de achamos com a relação
Como estamos no CASO 1 em , temos a seguinte figura:
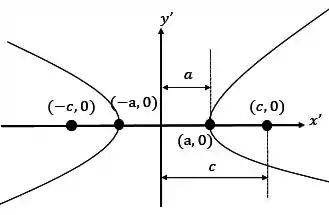
Teremos, então nossos vértices em
Nossos focos:
As assíntotas em são:
Por fim a excentricidade:
Achamos tudo o que precisávamos, MAS em e nossa resposta deve ser em . Para isso, vamos utilizar as relações:
Para muda para o sistema
Vértices:
Focos:
Assíntotas:
E a excentricidade não muda já que não depende de :
Uhullll!!! Terminamos!!
