Nas cônicas da figura os focos da hipérbole são vértices da elipse, os focos da elipse são vértices da hipérbole e o foco da parábola é um vértice da elipse. Sabendo que a equação da elipse é
determine as equações da parábola e da hipérbole.
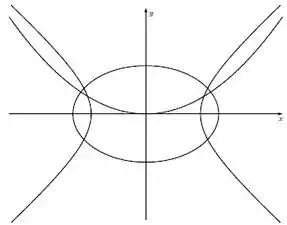
Passo 1
Primeiro vamos encontrar o da elipse, pois ele define onde está o foco dela.
Da equação da elipse, sabemos que e , logo, como :
Já o da elipse define onde está o seu vértice:
Passo 2
Belezinha, o problema falou pra gente que o foco da elipse é o vértice da hipérbole e o vértice da elipse é o foco da hipérbole .
Então na hipérbole, e . Bora encontrar o :
Então a equação da hipérbole é:
Passo 3
O foco da parábola vai ser o outro vértice da elipse, ou seja, . Então .
Substituindo na expressão da parábola:
Resposta
Hipérbole:
Parábola: