Considere a hipérbole de equação
Determine
a) As coordenadas de seus vértices e .
b) As coordenadas de seus focos e .
c) As equações de suas assíntotas e .
Passo 1
Primeiro vamos brincar com a equação dessa hipérbole. Completando os quadrados vamos ter
Dividindo tudo por :
Os parâmetros geométricos da hipérbole, então, são , e . O centro dela é o ponto (como vemos pela equação, ela não está centrada na origem) e seu eixo focal é paralelo ao eixo , que está positivo.
Passo 2
a) As coordenadas de nos vértices vão ser as mesmas que as de no centro, pois o eixo focal é paralelo ao eixo . Já as coordenadas de vão ser e , onde é a coordenada de em .
Logo, os vértices são e .
Passo 3
b) As coordenadas de nos focos também vão ser as mesmas que as de no centro, pois o eixo focal é paralelo ao eixo . Já as coordenadas de vão ser e .
Logo, os focos são e .
Passo 4
c) Igualando a equação da hipérbole a , temos
Vamos fatorar isso:
Resolvendo a parte esquerda:
Resolvendo a parte direita:
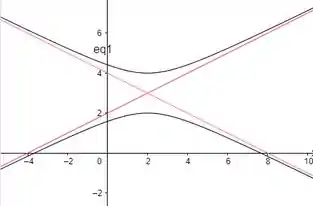
Abaixo temos o esboço da hipérbole e suas respectivas assíntotas em rosa
Resposta
a) e
b) e
c) e