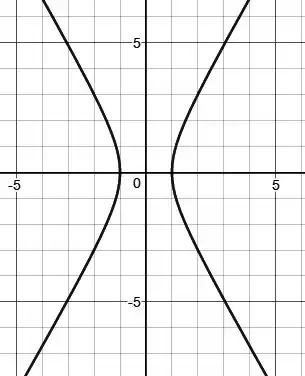
Determine os vértices, os focos, a excentricidade e as assíntotas das hipérboles dadas a seguir. Faça um esboço.
Passo 1
Opa!! Vamos começar a fazer exercícios com hipérboles?!

Nosso exercício consiste em determinarmos os elementos: vértices, focos. Excentricidade e as assíntotas da hipérboles. Bora começar!!!
Passo 2
a)
Em todas a cônicas o primeiro passo é deixar em uma das formas reduzidas para conseguirmos retirar os elementos. Vamos fazer isso, então:
Dividindo tudo por
Chegamos na forma canônica do CASO 1.
Assim, conseguimos retirar os valores de e .
Para acharmos o valor de vamos utilizar a seguinte relação:
Como estamos no CASO 1, teremos a seguinte figura:
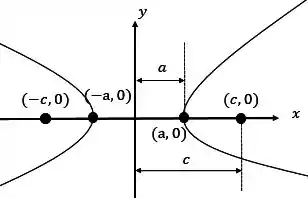
Assim, nosso focos e vértices serão:
As assíntotas serão:
E por fim, a excentricidade:
Substituindo os valores, teremos:
Fazendo um esboço, temos:
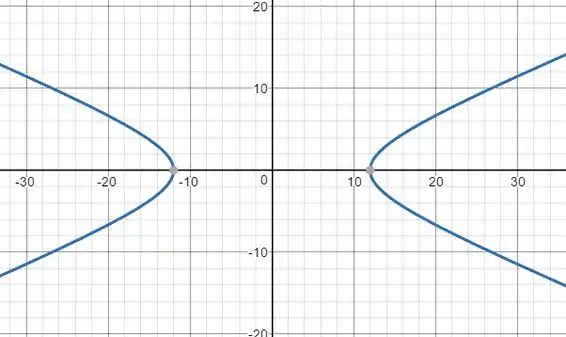
Passo 3
b)
Mesmo procedimento do item anterior:
Dividindo tudo por :
Estamos novamente no CASO 1. Então, teremos:
Então, nossos vértices, focos, assíntotas e excentricidade serão:
Subsituindo os valores:
Esboçando:
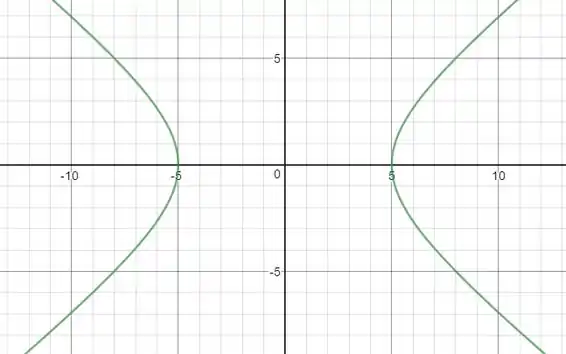
Passo 4
Passo 5
c)
Mesma coisa dos itens anteriores!! Então, dividindo tudo por , temos:
Agora, diferentemente dos outros dois itens estamos no CASO 2. Com a equação na forma reduzida conseguimos retirar os valores de e e ainda achar pela relação .
Como estamos no CASO 2 temos a seguinte figura:
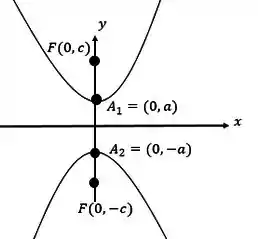
Então, nossos focos, vértices, assíntotas e excentricidade serão:
Substituindo os valores, temos:
Esboçando:
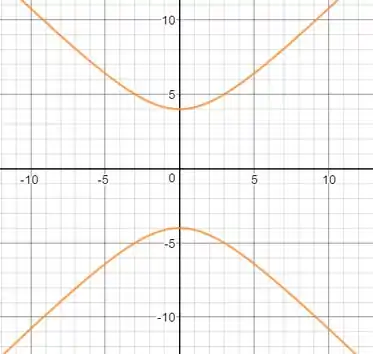
Passo 6
d)
Estamos novamente no CASO 2.Vamos achar então todos os parâmetros como fizemos antes:
Retirando os valores das constantes:
Sabemos do item anterior que nossos parâmetros, são:
Esboçando,
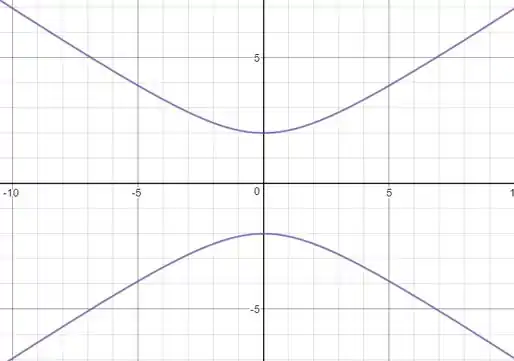
Passo 7
Ufaaa!! Está quase terminando, força!! Só falta mais esse item ;)
e)
Voltamos para o CASO 1.
Dos dois primeiros itens e da teoria sabemos que:
Subsituindo os valores encontrados, temos:
As assíntotas serão:
E por fim, a excentricidade:
Para terminar, esboço:
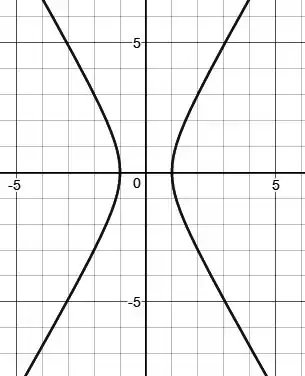
Resposta
a)
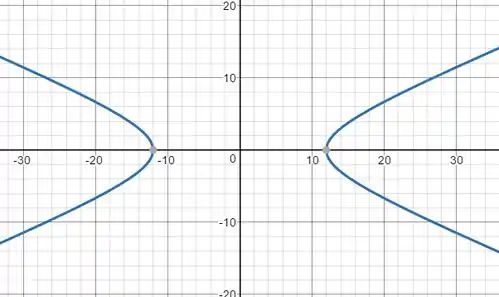
b)
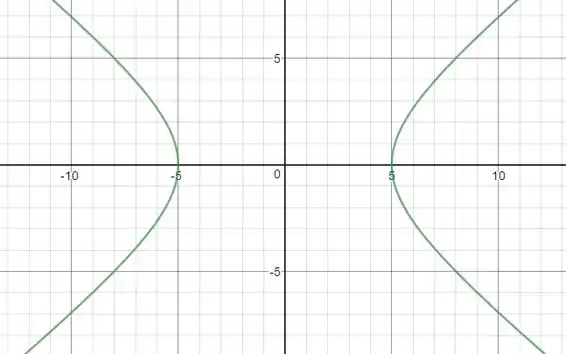
c)
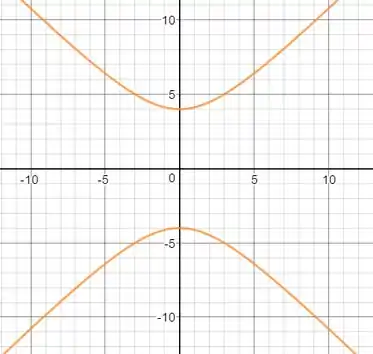
d)
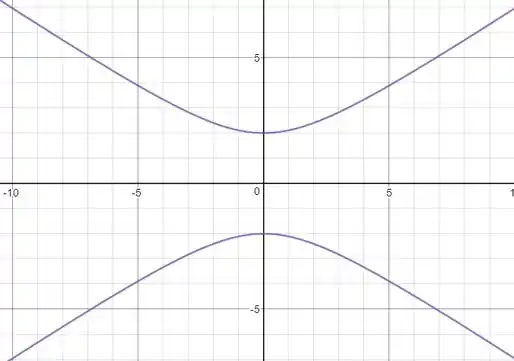
e)