Uma amostra de tamanho é extraída de uma população infinita, com distribuição normal com média e variância . Obtiveram-se com base nos dados desta amostra, dois intervalos de confiança para a nível e , sendo os limites superiores destes intervalos iguais a , respectivamente. Neste caso, a média amostral e variância da população valem, respectivamente
- 9 e 20
- 21 e 81
- 18 e 9
- 20 e 3
- 20 e 9
Passo 1
Fala pessoal, tudo bem com vocês? Vamos para mais uma questão de estatística. Calcular a média e variância de uma população, mas sabemos que em uma amostra de tamanho obtiveram-se dois intervalos de confiança para a nível e , sendo os limites superiores destes intervalos iguais a . Mas como usamos essas informações para calcularmos a média e a variância ?

Bem, vamos revisar a definiç��o de intervalo de confiança. O intervalo de confiança para a média amostral é definido por
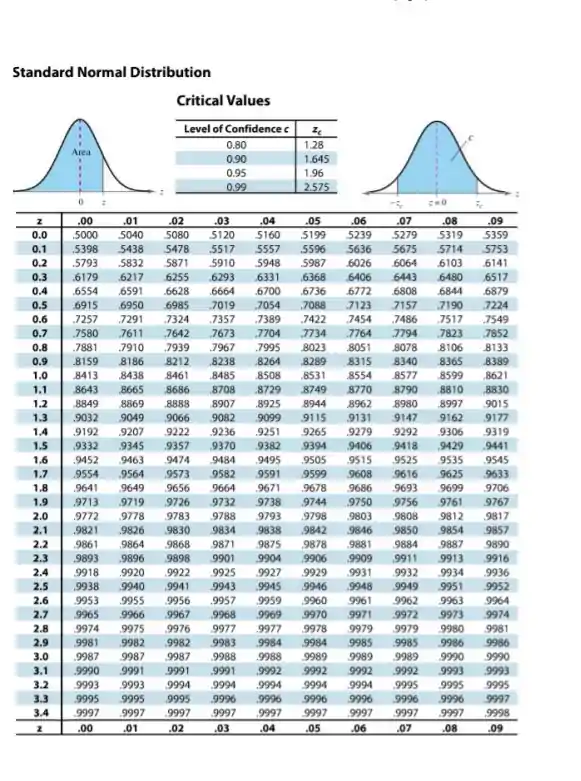
Onde é o nível de confiança. E coeficiente de confiança. Que pode ser encontrado utilizando a tabela
Como temos dois níveis de confiança . temos que os limites superiores desses intervalos de confiança são dados por
Mas sabemos quem é . É o número de amostras que no nosso caso é . Então chegamos a duas equações
Passo 2
Agora, precisamos calcular e
Pela tabela , esse valor é:
Substituindo nas nossas equações
Então temos
Subtraindo as duas equações temos:
Passo 3
Se , então . Substituindo essa valor em uma das equações
Ou seja descobrimos que e