O preço médio de um automóvel Palio ELX 1.0 quatro portas ano 2001 é R$ 18.000,00 (segundo Jornal Valor Econômico de 07/09/2019). Suponha que a variância estimada dos preços seja R$ 1.500,00 e o tamanho da amostra é carros. Pede-se:
a) Encontre o intervalo de confiança para a média ao nível de significância de 5% para os preços de Palios ELX 1.0 quatro portas ano 2001, supondo que os preços são normalmente distribuídos.
b) Encontre o intervalo de confiança para a variância ao nível de significância de 5%, para os preços de Palios ELX 1.0 quatro portas ano 2001, supondo que os preços são normalmente distribuídos.
Passo 1
O exercício deu para gente a média e variância estimada dos preços:
Com isso, podemos achar o desvio padrão da média:
Lembre-se sempre que o desvio padrão da média é o desvio padrão da amostra dividido pela raiz quadrada do número de elementos da amostra.
Para achar os intervalos de confiança vamos precisar do desvio padrão da média, por isso achei ele antes de discutir o problema!
Passo 2
No item (a), queremos um intervalo de confiança para a média e o enunciado disse que os preços seguem uma distribuição normal, de modo que vamos considerar que o preço médio também segue uma distribuição normal. Sua média será e o desvio padrão será o desvio padrão da média calculado no passo 1: .
Queremos achar um intervalo em torno da média que representa uma probabilidade de , já que o nível de significância é de . Para fazer isso, devemos introduzir uma nova variável:
Queremos que
Usando a simetria da distribuição de :
Além disso,
Nosso objetivo é achar o valor de tal que
Na tabela achamos:
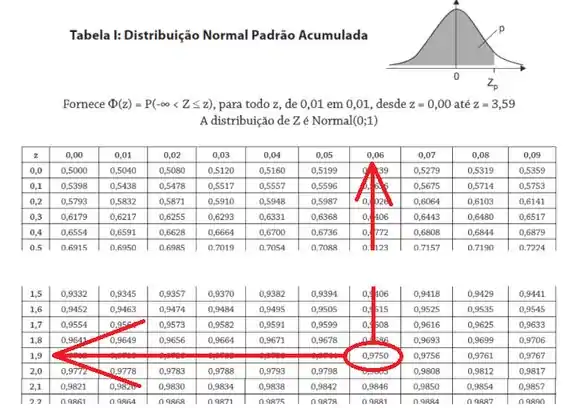
Passo 3
Os valores de que corresponde aos valores limites de são:
Substituindo os números:
Portanto, o intervalo de confiança para o preço médio é
Passo 4
No item (b) queremos saber o intervalo de confiança para a variância. Para isso, temos que lembrar que variável
segue uma distribuição de qui-quadrado com graus de liberdade. Essa é a distribuição que vamos usar para encontrar o intervalo de confiança!
Nesse caso, temos e , de modo que
A variável segue uma distribuição de qui-quadrado com graus de liberdade. A seguir faço um esboço de uma distribuição desse tipo:
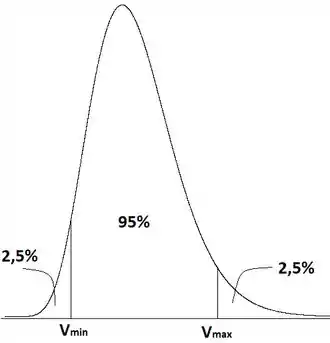
Queremos saber os valores e que delimitam um intervalo de de confiança (por isso separei para esquerda e para direita)! Para isso, devemos ter
Para achar esses limites, olhamos para a tabela na linha com 24 graus de liberdade:
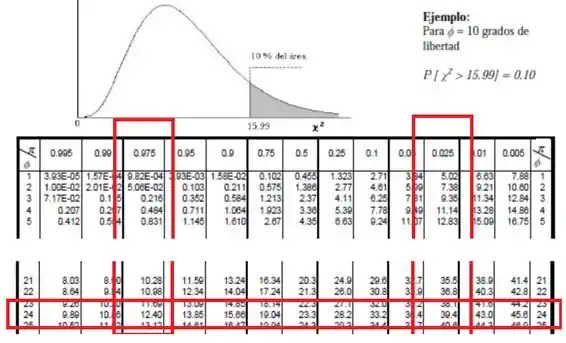
Com isso, achamos
Passo 5
Como e são inversamente proporcionais, o corresponde ao máximo de :
Analogamente, para o mínimo:
Portanto, o intervalo de confiança para a variância é
Com isso terminamos o problema 😊.
Resposta
a) .
b) .