USP, Sem Campus, Estatística, P1 - 2017, Questão Teste 2
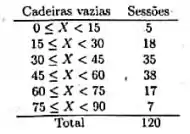
Para a tabela abaixo, o valor da média e variância das cadeiras vazias é:
- Média , variância
- Média , variância
- Média , variância
- Média , variância
- Média , variância
Passo 1
Fala pessoal, tudo bem com vocês? Vamos para mais uma questão de estatística. Calcular a média e variância das cadeiras vazias. Mas como calculamos esses valores em uma tabela de frequências?
Bem, primeiro precisamos calcular os valores médios de cada classe na tabela de frequência. Pois estes serão utilizados nos cálculos da média e variância. Bem temos as seguintes classes
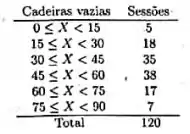
o valor médio da primeira classe é o valor do meio da classe. Como a primeira classe vai de
Logo, o valor do meio é .
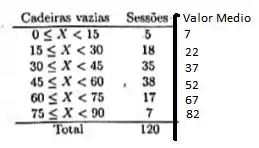
A seguir, temos a tabela de frequências com os valores médios de cada classe
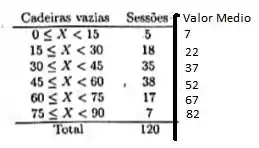
Passo 2
Agora que temos os valores médios de cada classe, podemos calcular a média de assentos vazios dessa tabela de frequência. Por definição, a média é dada por
Onde é a média da classe , e sua frequência. Consultando a nossa tabela modificada, temos que a média é dada por
Por fim, vamos calcular a variância. Ela é dada por,
No nosso caso, temos