Seja uma variável aleatória contínua que segue uma distribuição normal com média e variância , ambas desconhecidas. Seja , uma amostra de tamanho desta população. Pede-se que:

a) Calcule o intervalo de confiança ao nível de para a média, detalhando todos os passos necessários para construção deste .

b) Calcule o intervalo de confiança ao nível de para a variância, detalhando todos os passos necessários para a construção deste .

Observação: cálculos com 4 casas decimais.

Antes de prosseguir, precisamos de uma estimativa razoável para e . O estimador mais usual para é

Já para a variância, o melhor estimador é

O termo no lugar de no denominador aparece pois estamos tomando a variância amostral. Usando esses estimadores no lugar de e (que são desconhecidos), temos que

Além disso, como é a soma de variáveis aleatórias que obedecem a uma distribuição normal, também deve obedecer a uma distribuição normal. Como já temos e , podemos construir essa distribuição.

No item (a), devemos achar o com confiança de para a variável (média amostral). Isso significa que devemos achar qual o intervalo de valores de em torno da média que correspondem a uma probabilidade de :

Isso significa que a área da região pintada deve corresponder a .

Para resolver esse problema, devemos normalizar a distribuição definindo uma nova variável aleatória dada por

Essa variável terá uma distribuição normal com média e variância :

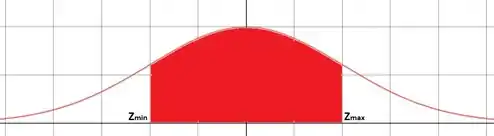
Como a distribuição é simétrica, é fácil perceber que . Para que a confiança seja de :

Para determinar o valor de , temos que olhar para a tabela da distribuição normal padrão acumulada. Vou usar a versão que foi dada na própria prova:

Essa tabela pode ser fornecida de várias formas, por isso é bem importante saber qual a convenção que está sendo utilizada. Na tabela fornecida na prova, a distribuição acumulada representa a probabilidade de . Vamos adaptar nosso problema a essa situação:

Mas note que , pois representa metade da distribuição (que é simétrica). Assim,

Olhando na tabela:

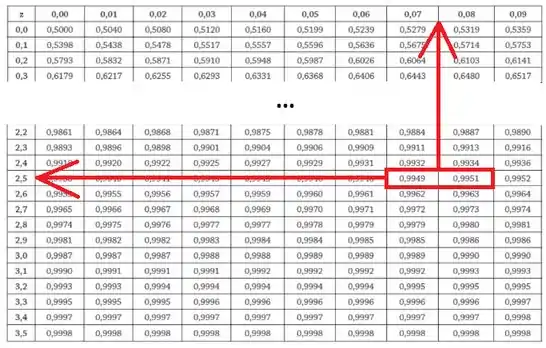
Portanto,

Daí, basta isolar como função de :

Como , temos que

Portanto,

Portanto, o intervalo de confiança é

Agora vamos ao item (b). Queremos achar o intervalo de confiança para a variância. Nos passos anteriores calculamos a variância amostral que representa um estimador da variância :

No formulário foi dada a relação pivotal:

Isso significa que a variável segue uma distribuição do tipo . A ideia aqui vai ser bem parecida com o que estamos fazendo para a variável no item (a) que seguia uma distribuição normal, só que agora vamos olhar para uma distribuição de qui-quadrado!

Vamos considerar uma distribuição de qui-quadrado como a esboçada a seguir:

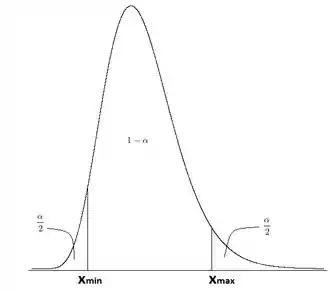
A probabilidade que é e a probabilidade que também é . Como queremos um intervalo com confiança de , a probabilidade de estar entre e deve ser de , de modo que

Portanto, devemos ter

Agora nossa tarefa é achar e . Para isso, vamos recorrer a tabela de distribuições de qui-quadrado fornecido na prova:

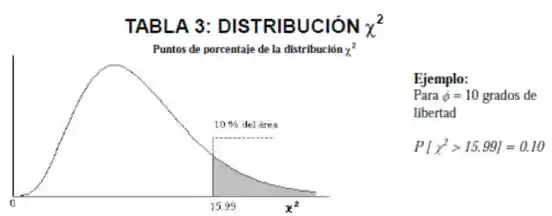
Para ler tabela temos que perceber que cada linha representa o número de graus de liberdade da distribuição. No nosso caso, temos . Destaquei essa linha na tabela. Já as colunas representam as probabilidades para que , onde é dado da tabela.

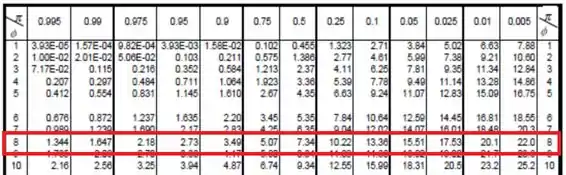
Vamos olhar primeiro para a condição . Olhando a tabela, vemos que isso acontece na última coluna, de modo que

Para achar , vamos ter que brincar um pouco com a condição :

Logo,

Olhando na tabela (primeira coluna), achamos

Com isso o problema está praticamente resolvido. Isolando :

Como :

Note que como é inversamente proporcional a , corresponderá a , e vice-versa. Portanto,

Desta forma, o intervalo de confiança para a variância com confiança de :

E assim terminamos o problema 😊.