Seja uma v.a. com distribuição qui-quadrado com graus de liberdade. Qual é a ?

Sabemos que:

Vamos olhar a parte da nossa tabela que tem :

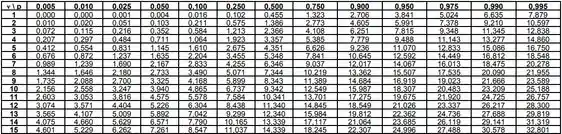
Agora, nessa linha do , temos que achar a probabilidade pedida:

Opa, temos um ali! E se fossemos escrever esse cara com duas casas decimais arredondaríamos para . Então essa aí é a que queremos! Agora temos que ver o correspondente:

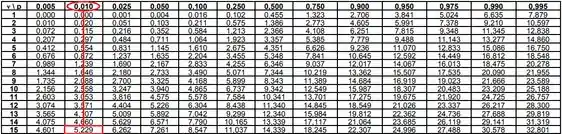
Então podemos afirmar que:

Mas calmaê! Pode ser que sua prova tenha outro tipo de tabela, essa que nós mostramos nos dá , a probabilidade acumulada até um certo qui-quadrado, ou seja, menores que esse qui-quadrado. Mas às vezes, a tabela que disponibilizam pra gente é , ou seja, o contrário!

Vamos dar uma olhada em como seria se só tivéssemos esse segundo tipo de tabela:

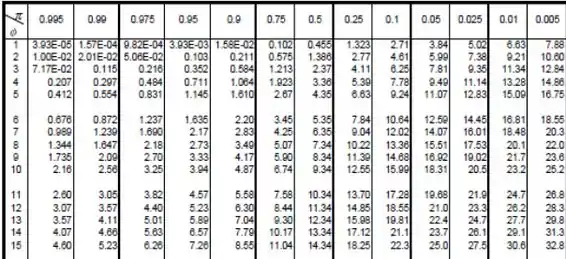
Nosso grau de liberdade agora tá sendo denotado por , e sabemos que . Agora temos que procurar a probabilidade na linha que tem como grau de liberdade:

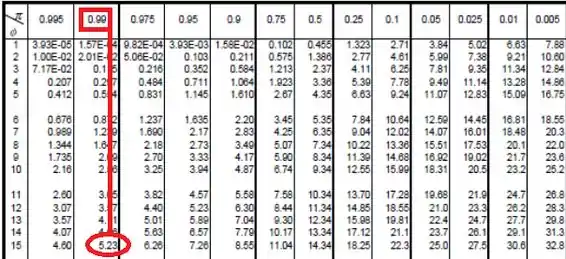
Mas lembra que essa probabilidade é da tabela tipo ? Então isso aí que vimos quer dizer que:

E a questão tá pedindo pra gente:

Ou seja, a complementar da que a gente tem na tabela! Então:

Fique sempre atento a qual dos dois tipos de tabela sua prova vai disponibilizar, se são das probabilidades acumuladas maiores ou menores que um certo !