01) Um bloco de massa está apoiado, em equilíbrio, sobre uma mola de constante elástica . Subitamente, um segundo bloco de massa é apoiado, sem choque, sobre o primeiro bloco. Pede-se:
a) A deformação inicial da mola.
b) O deslocamento vertical correspondente à máxima velocidade dos blocos.
c) A máxima velocidade dos blocos.
d) A máxima deformação da mola.
e) A máxima força exercida pela mola sobre os dois blocos.
Passo 1
Faaala gente bonita do Responde Aí, como vocês estão?
a) Nessa questão temos inicialmente um bloco, de massa , apoiado sobre uma mola. Isso significa que inicialmente a mola já está deformada, vamos chamar essa deformação de , beleza?
Aí, do nada, coloca-se um outro bloquinho, de massa , em cima desse conjunto. Naturalmente, o conjunto inteiro vai começar a oscilar, em um movimento tipo MHS.

Pra começar bem, devemos determinar a deformação inicial da mola.
Bom, bora desenhar o diagrama de forças pro nosso bloco no instante inicial. Temos apenas a força peso e a força elástica atuando sobre ele, que está em equilíbrio. Daí:
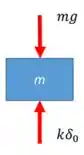
Pela lei de Newton, temos:
Prontinho! Essa é a deformação inicial da mola.
Passo 2
b) Nesse item devemos determinar o deslocamento vertical quando a velocidade é máxima.
Pô, comentamos anteriormente que quando apoiamos o bloco de massa , o conjunto passa a realizar um movimento oscilatório. Mas, em qual momento do movimento oscilatório temos velocidade máxima?

Cara, é justamente quando a aceleração for nula!
Imagina só, o conjunto está sendo acelerado, mas a aceleração vai diminuindo. Enquanto tivermos o conjunto ganha velocidade.
Em um dado instante, temos , e logo após isso a aceleração passa a ser negativa, com a velocidade do conjunto diminuindo.
Assim, a máxima velocidade alcançada é exatamente quando , sacou?
Então tá, bora calcular o deslocamento quando . Desenhando o diagrama de forças do conjunto, temos:
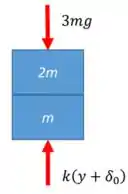
Nota que já escrevemos como sendo o deslocamento em relação ao nível inicial .
Daí, usando a lei de Newton, temos:
Do item a), sabemos que:
Substituindo, temos:
Como queremos o deslocamento quando , vem:
Bouaa! Matamos mais um item 😊
Passo 3
c) Devemos determinar a máxima velocidade dos blocos.
No item anterior, vimos que essa máxima velocidade ocorre justamente quando , o que implica
Beleza, mas e agora?
Bom, a gente pode tentar uma abordagem por energia, que é um ótimo caminho já que só atuam forças conservativas. Mas, tem também uma ideia bem legal pra gente trabalhar nesse exercício.
Sabemos que:
Só que a expressão que calculamos no item anterior para a aceleração está em função de , e não de . Lembra?
Tem um truque bem legal pra resolver esse problema, podemos fazer:
Mas,
Assim, chegamos que:
Top né? Conseguimos eliminar o tempo da jogada. Então, vamos igualar nossas expressões:
Essa equação é separável, então temos:
Integrando dos dois lados, temos:
Pra eliminar a constante basta lembrar que, quando , . Assim:
Logo:
Agora é só dar o golpe final. Sabemos que é máxima quando . Assim:
Bouaaaa! É uma forma com um trabalho mais algébrico para calcular a velocidade.

Passo 4
d) Agora devemos calcular a máxima deformação da mola.
Mas, em que instante que ocorre ? Tipo, qual a característica física desse instante?

É justamente quando a velocidade zera.
Pensa comigo, enquanto tivermos a deformação está aumentando, porém, a velocidade vai diminuindo. Em um certo momento ocorre inversão do sentido do deslocamento, ou seja, . Nesse momento, foi alcançado o . Entendeu?
Massa! No item anterior calculamos uma expressão para :
Se , temos:
Como queremos que a deformação seja máxima, a solução não nos interessa. Logo:
Essa é a resposta final??
Nãooo haha. É que a questão pede a deformação máxima da mola, é a amplitude máxima da oscilação. Pra calcular a deformação máxima devemos considerar que, inicialmente, ela já possui uma deformação . Assim:
Agora simm! Essa é a resposta do item d) 😊
Passo 5
e) Pra finalizar mais uma questaozita, devemos calcular a força máxima exercida pela mola no conjunto.
Pô, pensa comigo, sabemos que:
é uma constante, logo a força é máxima quando tivermos .
Portanto, usando o resultado do item anterior, temos:
Logo:
Aeee, terminamos! Foi bem legal essa questão, né?
Espero que vocês tenham gostado, até a próxima pessoal 😉
Resposta
a)
b)
c)
d)
e)