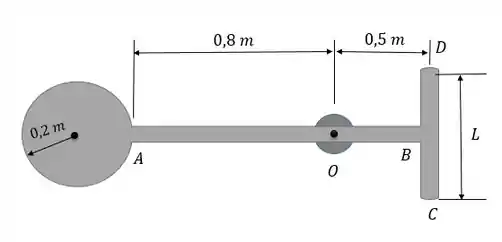
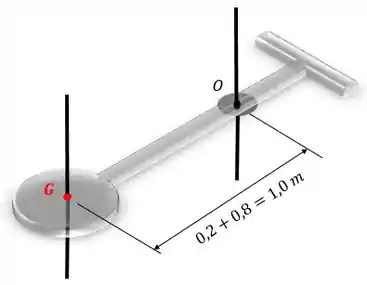
O sistema consiste num disco de e de duas barras delgadas e , cada uma com . Se , determine o momento de inércia do sistema em relação ao eixo que é perpendicular à página e passa por . Suponha que as barras e o disco são homogêneos.
Passo 1
Vamos começar calculando o momento de inércia da barra com relação a um eixo que passe pelo seu centro de massa:
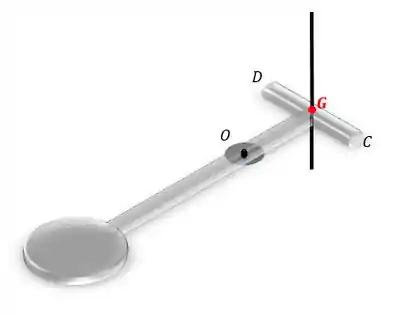
O momento de inércia de uma barra em relação a um eixo que passa pelo seu centro de gravidade é tabelado:
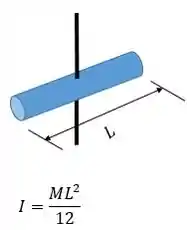
Então:
Qual é a massa da barra ? Sabemos que ela possui por metro. Se esta barra tem , então:
Então, seu momento de inércia será:
Passo 2
Repare que o exercício quer o momento de inércia com relação a um eixo que passa pelo ponto . Para calcular isso, temos que usar o teorema dos eixos paralelos:
Qual será a distância entre os eixos?
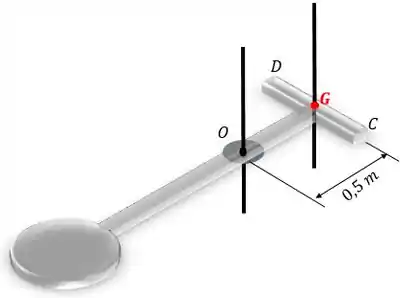
Então:
Passo 3
Agora vamos calcular o momento de inércia da barra com relação a um eixo que passa pelo seu centro de massa (que corresponde à metade do seu comprimento):
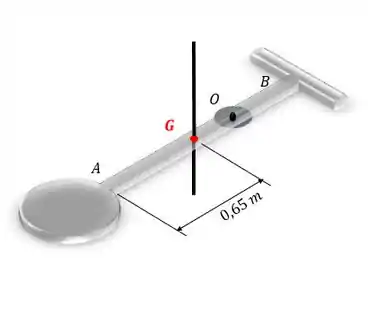
O momento de inércia de uma barra delgada nós já vimos que é:
Mas qual é o valor da massa dessa barra? Nós vamos calcular da mesma maneira que calculamos anteriormente. A barra também posssui para cada metro de barra e no total ela tem , então:
O momento de inércia da barra será:
Passo 4
Agora temos que calcular o momento de inércia dessa barra com relação ao eixo que passa pelo ponto :
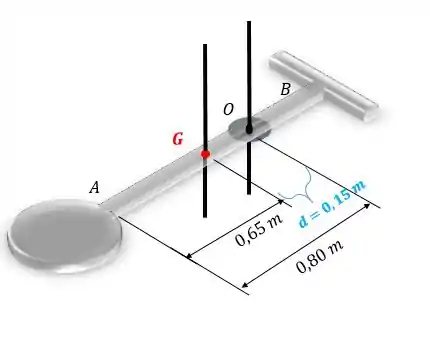
Então:
Passo 5
Agora vamos calcular o momento de inércia da placa circular com relação a esse eixo aqui:
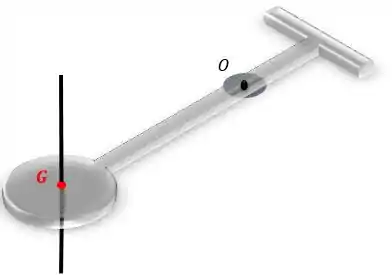
O momento de inércia de uma placa circular com relação ao eixo que passa pelo seu centro de gravidade também é tabelado:
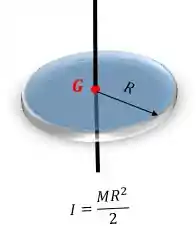
Então, no nosso caso teremos:
A nossa placa tem e possui raio de :
Passo 6
O que queremos é o momento de inércia com relação ao eixo que passa pelo ponto , então vamos ter que usar o teorema dos eixos paralelos:
Então:
Passo 7
Para calcular o momento de inércia do conjunto de peças, temos que somar todos os momentos que achamos para cada parte que compõe o sistema: