Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Dinâmica de Corpos Rígidos

Ver Teoria
Exercício 712345689

Enunciado

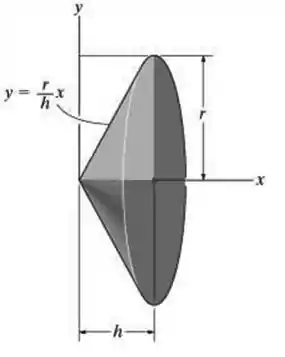
O cone circular reto é formado pela revolução, em torno do eixo x , da área cinza-escuro. Determine o momento de inércia I x e expresse o resultado em termos da massa total m do cone. Considere que o cone tem densidade constante ρ .

Passo 1

Para resolver este problema vamos usar o método do disco elementar, ou seja, vamos criar um disco dentro do nosso cone com raio y e uma espessura infinitesimal d x . Com isso, sabemos que o nosso volume será:

d V = π y 2 d x

Vamos começar calculando a massa deste sólido e para isso temos que saber que:

m = ∫ d m

Mas como se calcula esse elemento de massa infinitesimal d m ?

d m = ρ d V

Opa, vamos substituir o nosso d V neste equação:

d m = ρ d V   →         d m = ρ π y 2 d x

Então, a nossa integral vai ficar:

m = ∫ d m     →         m = ∫ ρ π y 2 d x

Vamos passar as nossas constantes para o lado de fora da equação:

m = π ρ ∫ y 2 d x

E agora vamos integrar ao longo da altura do cilindro de modo que o nosso disco percorra toda a altura do cone:

m = π ρ ∫ 0 h y 2 d x

Perceba que na figura foi dada a equação do cone:

y = r x h

Vamos substituir o y da nossa integral:

m = π ρ ∫ 0 h r x h 2 d x

Repare que r e h também são constantes:

m = π ρ r h 2 ∫ 0 h x 2 d x

Agora é só resolver:

m = π ρ r h 2 ∫ 0 h x 2 d x         →           m = π ρ r h 2 x 3 3 | 0 h

Então:

m = π ρ r h 2 h 3 3

Vamos ter que:

m = π ρ r 2 h 3

Como o enunciado pede o momento de inércia em função da massa m , vamos isolar ρ :

ρ = 3 m π r 2 h

Passo 2

Nosso próximo passo é calcular o momento de inércia em relação ao eixo x . Para isso, temos que calcular o momento de inércia do disco de espessura infinitesimal:

I x = ∫ r 2 d m

Mas sabemos que o momento de inércia de um cilindro em relação ao seu eixo longitudinal é:

I =   m R 2 2

Como o disco que criamos é um cilindro só que de espessura bem pequena, é só derivarmos o momento de inércia do cilindro que é sempre a mesma para o eixo longitudinal:

d I x = d m R 2 2

Repare que o raio R é constante, por isso só derivamos a massa.

Nós já sabemos que:

d m = ρ π y 2 d x

Então d I x vai ser:

d I x = ( ρ π y 2 d x ) R 2 2

Repare que o raio r = y do nosso disco varia conforme ele percorre toda a altura do cone, então:

d I x = ( ρ π y 2 d x ) y 2 2

Vamos ter que:

d I x = ρ π y 4 d x 2

No passo 1 achamos que ρ :

ρ = 3 m π r 2 h

Vamos ter que d I x :

d I x = 3 m π r 2 h π y 4 d x 2

Passo 3

Pronto! Agora é só integrarmos dos dois lados:

∫ d I x = ∫ 3 m π r 2 h π y 4 d x 2

Vamos tirar nossas constantes para fora da integral:

I x = 3 m π r 2 h π 2 ∫ y 4 d x

Repare que dá para simplificar essas constantes:

I x = 3 m 2 r 2 h ∫ y 4 d x

Nós sabemos que a equação do cone é: y = r x h

Então, a nossa integral ao longo da altura h será:

I x = 3 m 2 r 2 h ∫ 0 h r x h 4 d x

Vamos tirar as constantes para fora da integral e depois simplificar:

I x = 3 m 2 r 2 h r h 4 ∫ 0 h x 4 d x       →           I x = 3 m r 2 2 h 5 ∫ 0 h x 4 d x

Vamos ter que:

I x = 3 m r 2 2 h 5 x 5 5 | 0 h

I x = 3 m r 2 2 h 5 h 5 5

Vamos arrumar nossa resposta:

I x = 3 m r 2 10

Resposta

I x = 3 m r 2 10

Exercícios de Livros Relacionados

Utilize os resultados do Prob. 7/55 e determine a quantidade de movimento angular H g dobrada daquele problema em relação ao seu centro de massa G utilizando os eixos de referência fornecidos.
A placa retangular, com uma massa de 3 kg e uma pequena espessura uniforme, está soldada no ângulo de 45º ao eixos vertical, que gira com a velocidade angular de 20 ⋅ πr a d / s . Determine a quantida
O mecanismo para controlar a implantação de um painel solar de uma nave espacial a partir da posição A para a posição B está sendo projetado. Determine a expressão vetorial para o único ângulo θ de ro
O pequeno motor M é articulado em relação ao eixo x através de O e transmite ao seu eixo AO uma velocidade constante p rad/s no sentido mostrado, em relação á sua carcaça. O conjunto inteiro é, em seg
O disco circular de 6 kg e o eixo associado giram a uma velocidade angular constante ω = 10000r p m . Se o centro de massa do disco está deslocado do centro em 0,05 mm, determine o módulo das forças h