O cilindro sólido tem raio e altura h. O material de que ele é feito tem uma densidade que varia com a distância ao centro de acordo com a expressão , onde e são constantes. Determine a massa do cilindro e seu momento de inércia em relação ao eixo .

Para resolver este problema vamos usar o método da casca elementar, ou seja, vamos criar uma casca dentro do nosso cilindro com altura , raio e uma espessura infinitesimal :

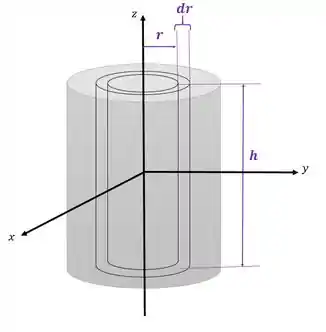
Com isso, sabemos que o nosso volume será:

Vamos começar calculando a massa deste cilindro e para isso temos que saber que:

Mas não esqueça que:

Opa, vamos substituir o nosso neste equação:

Então, a nossa integral vai ficar:

Mas foi dito no enunciado que , então:

Vamos passar as nossas constantes para o lado de fora da equação:

E agora vamos integrar ao longo do raio do cilindro de modo que a nossa casca vá de a :

Vamos ter que:

Podemos arrumar um pouco mais isso: