Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Dinâmica de Corpos Rígidos

Ver Teoria
Exercício 123456789

Enunciado

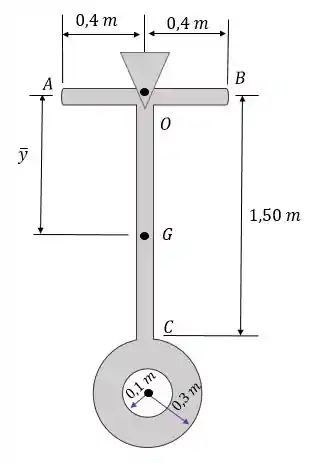
O pêndulo consiste em duas barras delgadas e homogêneas A B e O C , cada uma delas com 3   k g / m e uma placa também homogênea com 12   k g / m 2 . Determine a ) a posição y -   do centro de massa G do pêndulo e, a seguir, b ) seu momento de inércia em relação a um eixo que é perpendicular à página e passa por G .

Passo 1

Vamos começar calculando a posição y - do centro de massa G do pêndulo. Para isso, temos que puxar lá da memória que para calcular a posição y - do centro de massa usamos a seguinte equação:

y - = ∑ y G i m i ∑ m i

Calma! Primeiro temos que definir onde está o nosso eixo e marcar a partir dele a coordenada y de cada centro de massa. Mas como assim para cada centro de massa? É porque para facilitar a nossa vida, vamos dividir nossa peça em duas barras ( A B e O C ) e na placa circular com furo:

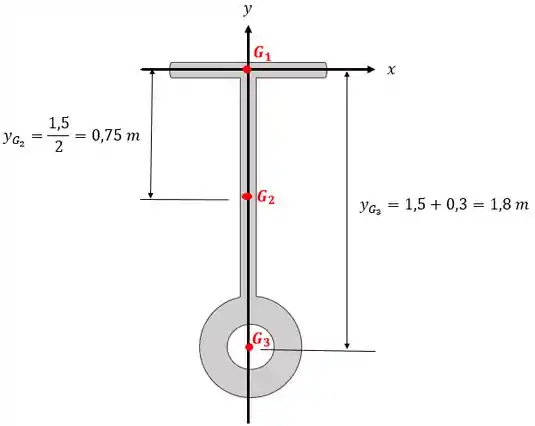
Repare que a coordenada y G 1 é zero.

Então, vamos ter que:

y - = y G 1 m 1 + y G 2 m 2 + y G 3 m 3 m 1 + m 2 + m 3

Antes temos que calcular as massas de cada parte que compõe o corpo. Vamos começar pela barra A B que possui 3   k g por metro de barra, como a barra tem 0,8   m , teremos que:

m 1 = 3 0,8         →             m 1 = 2,4   k g

A barra O C também possui 3   k g por metro de barra, como a barra tem 1,5   m :

m 2 = 3 1,5         →           m 2 = 4,5   k g

Agora vamos calcular a massa da placa circular, sabendo que ela possui 12   k g / m 2 . Temos que calcular a área desta placa, para isso vamos subtrair a área do círculo menor ( A m e n o r ) da área do círculo maior ( A m a i o r ):

A P l a c a = A m a i o r -   A m e n o r       →           A P l a c a = π 0,3 2 - π ( 0,1 2 )

A P l a c a = 0,25   m 2

Então, a massa da placa é:

m 3 = 12 0,25     →           m 3 = 3   k g

Pronto! Agora sim podemos calcular a posição do centro de massa:

y - = y G 1 m 1 + y G 2 m 2 + y G 3 m 3 m 1 + m 2 + m 3       →           y - = 0,75 ( 4,5 ) + 1,8 ( 3 ) 2,4 + 4,5 + 3

y - = 0,89   m

Passo 2

Agora temos que calcular o momento de inércia de cada parte que compõe o corpo com relação ao eixo que passa por este ponto G . Já viu que vamos ter que usar o teorema dos eixos paralelos, né?

Vamos começar pela barra A B , calculando o momento de inércia com relação ao eixo que passa pelo centro de massa desta barra:

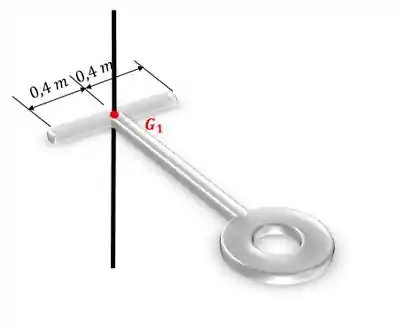
Sabemos que o momento de inércia de uma barra com relação a um eixo que passe pelo seu centro de massa é:

I G = M L 2 12

Então:

I G 1 = m 1 L 1 2 12         →             I G 1 = 2,4   ( 0,8 2 ) 12

I G 1 = 0,128   k g . m 2  

Agora vamos usar o teorema dos eixos paralelos para achar o momento de inércia com relação a um eixo que passe por G :

I G = I G 1 + m 1 d 2

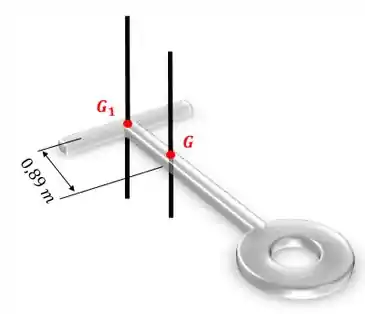
Repare que a distância d entre eixos paralelos é de 0,89   m :

I G = 0,128   + 2,4 ( 0,89 ) 2

I G = 2,03   k g . m 2    

Passo 3

Agora vamos partir para a barra O C e começar calculando o momento de inércia com relação a um eixo que passa pelo centro de gravidade desta barra (que corresponde à metade do seu comprimento):

I G 2 = m 2 L 2 2 12         →             I G 2 = 4,5 ( 1,5 ) 2 12

I G 2 = 0,84   k g . m 2

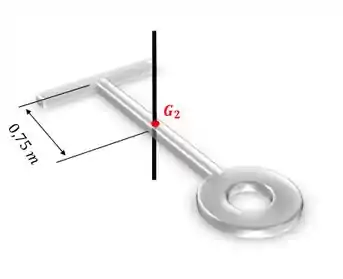
Agora vamos calcular o momento de inércia com relação ao eixo que passa pelo ponto G :

I G = I G 2 + m 2 d 2       →           I G = 0,84   + 4,5 ( 0,14 ) 2      

I G = 0,93   k g . m 2

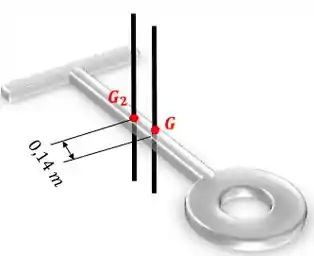
Passo 4

Agora temos que calcular o momento de inércia da placa circular com o furo com relação ao eixo que passa pelo seu centro de massa:

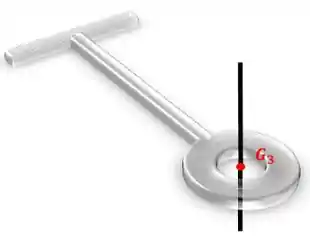
Uma placa circular com um furo no meio tem o momento de inércia tabelado:

I = M 2 ( R m a i o r 2 - R m e n o r 2 )

No nosso caso, temos que R m a i o r = 0,3   m e R m e n o r = 0,1   m :

  I G 3 = m 3 2 R m a i o r 2 - R m e n o r 2     →           I G 3 = 3 2 0,3 3 - 0,1 2    

  I G 3 = 0,12   k g . m 2  

Para calcular o momento de inércia com relação ao eixo que passa pelo ponto G , teremos:

I G = I G 3 + m 3 d 2       →           I G = 0,12   + 3 ( 0,91 ) 2      

I G = 2,6   k g . m 2

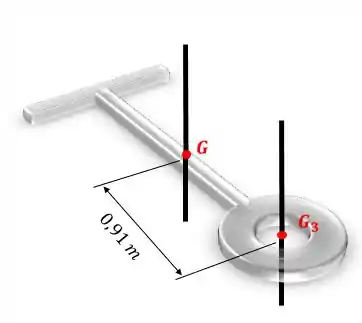
Passo 5

Nós calculamos o momento de inércia de todas as partes que compõe o nosso corpo, então para achar o momento de inércia do pêndulo com relação ao eixo que passa pelo ponto G é só somar tudo:

I G P ê n d u l o = 2,03   + 0,93   + 2,6  

I G P ê n d u l o = 5,6   k g . m 2    

Resposta

a )   y - = 0,89   m

b )   I G P ê n d u l o = 5,6   k g . m 2  

Exercícios de Livros Relacionados

Utilize os resultados do Prob. 7/55 e determine a quantidade de movimento angular H g dobrada daquele problema em relação ao seu centro de massa G utilizando os eixos de referência fornecidos.
A placa retangular, com uma massa de 3 kg e uma pequena espessura uniforme, está soldada no ângulo de 45º ao eixos vertical, que gira com a velocidade angular de 20 ⋅ πr a d / s . Determine a quantida
O mecanismo para controlar a implantação de um painel solar de uma nave espacial a partir da posição A para a posição B está sendo projetado. Determine a expressão vetorial para o único ângulo θ de ro
O pequeno motor M é articulado em relação ao eixo x através de O e transmite ao seu eixo AO uma velocidade constante p rad/s no sentido mostrado, em relação á sua carcaça. O conjunto inteiro é, em seg
O disco circular de 6 kg e o eixo associado giram a uma velocidade angular constante ω = 10000r p m . Se o centro de massa do disco está deslocado do centro em 0,05 mm, determine o módulo das forças h