Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Dinâmica de Corpos Rígidos

Ver Teoria
Exercício 213456789

Enunciado

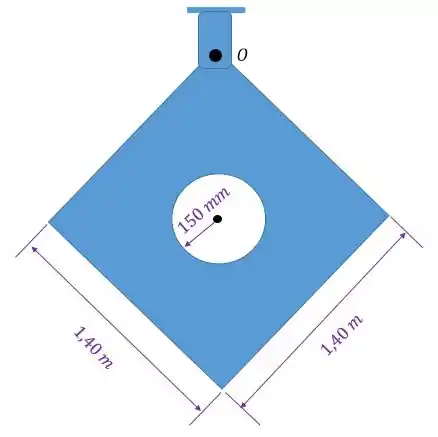
Determine o momento de inércia em relação a um eixo que é perpendicular à página e passa pelo pino em O . A placa fina tem um furo central e espessura de 50 mm. O material tem densidade ρ = 50   k g / m 3 .

Passo 1

Vamos começar calculando o momento de inércia da placa quadrada com relação ao seu centro de gravidade. Mas para isso vamos considerar que a placa seja inteira, ou seja, não tenha nenhum furo:

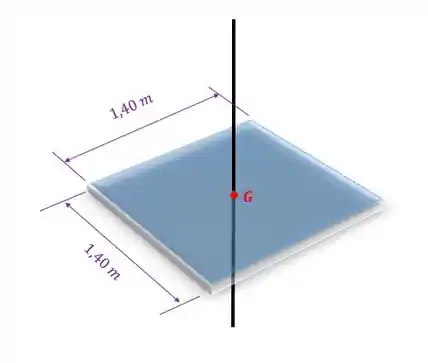
A fórmula do momento de inércia com relação a um eixo que passe no centro de gravidade de uma placa é tabelado:

I G = M ( a 2 + b 2 ) 12

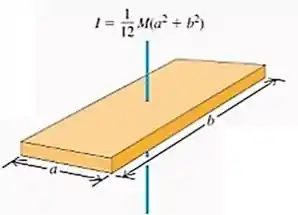
Nossa placa é quadrada, então b = a :

I G = M a 2 + a 2 12         →         I G = M ( 2 a 2 ) 12

I G = M a 2 6

Mas quanto vale a massa da nossa placa? Sabemos que o material tem densidade ρ = 50   k g / m 3 e a fórmula da densidade é:

ρ = M V

Onde, M é a massa e V é o volume do corpo. A nossa placa é quadrada de lado 1,40   m e tem uma espessura de 50   m m = 0,05   m , então seu volume V será:

V = 1,40 1,40 0,05 = 0,098   m 3

Então, a massa será:

ρ = M V         →           50 = M 0,098

M = 4,9   k g

Agora sim podemos calcular o momento de inércia com relação ao eixo que passa pelo seu centro de gravidade:

I G = M a 2 6       →           I G = 4,9 ( 1,4 ) 2 6

I G = 1,6   k g . m 2

Passo 2

Repare que o exercício quer o momento de inércia com relação a um eixo que passa pelo pino em O . Para isso, temos que aplicar o teorema dos eixos paralelos:

I O = I G + m d 2

Qual será a nossa distância d neste caso?

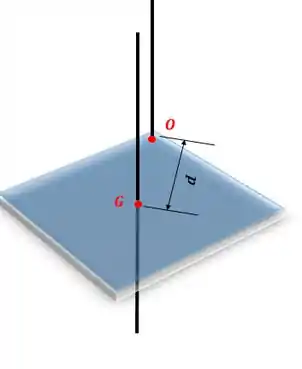
É a distância entre os eixos. Repare que vamos ter o seguinte triângulo retângulo:

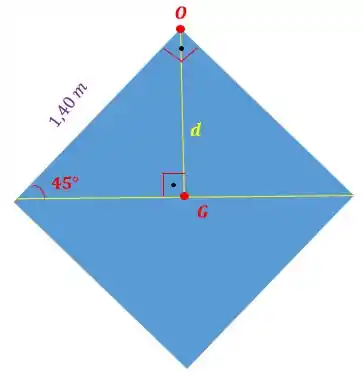
Então, a distância d será:

s e n   45 ° = d 1,40       →         d = 0,9899   m

Já temos tudo o que precisamos para calcular o momento de inércia da placa com relação ao eixo que passa pelo ponto O :

I O = I G + m d 2       →           I O Q u a d r a d o = 1,6   + 4,9 ( 0,9899 ) 2

I O Q u a d r a d o = 6,40   k g . m 2

Passo 3

Agora vamos esquecer que existe a placa quadrada e vamos olhar apenas para o furo central imaginando que ele seja um círculo maciço e não um vazio. Com isso, vamos calcular o momento de inércia deste círculo central com relação a um eixo que passe pelo seu centro de gravidade:

O momento de inércia de uma placa circular também é tabelado e vale:

I G = M R 2 2

Como vamos calcular a massa dessa placa circular? Do mesmo jeito que calculamos a massa da placa quadrada, pois o material é o mesmo e a densidade vai continuar sendo ρ = 50   k g / m 3 , então:

ρ = M V

Para saber o volume da placa circular, temos que tratar como um cilindro de espessura e =   50   m m :

V c i l i n d r o = π R 2 e         →           V = π 0,150 2 ( 0,05 )

V = 3,53   m 3

Então, a massa da placa circular será:

ρ = M V       →         50 = M 3,53

M = 0,1767   k g

Agora podemos calcular o momento de inércia com relação ao eixo que passa pelo centro de gravidade:

I G = M R 2 2         →           I G = 0,1767 ( 0,15 ) 2 2

I G = 1,988   x   10 - 3   k g . m 2

Passo 4

Agora temos que calcular o momento de inércia dessa placa circular com relação a um eixo que passe pelo ponto O . Para isso, vamos aplicar o teorema dos eixos paralelos de novo:

I O = I G + m d 2

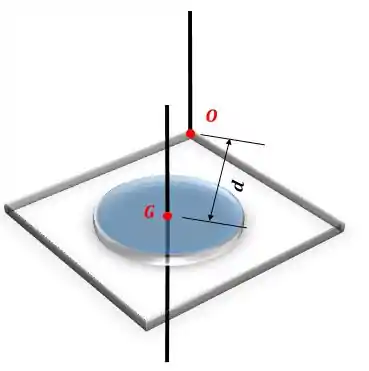
Repare que a distância d continua a mesma, pois o centro de gravidade da placa quadrada coincide com o centro de gravidade da placa circular (ponto G ):

d = 0,9899   m

Então:

I O = I G + m d 2         →             I O C i r c u l o = 1,988   x   10 - 3 + 0,1767 ( 0,9899 ) 2

I O C i r c u l o = 0,175   k g . m 2  

Passo 5

Nós calculamos o momento de inércia da placa quadrada e do círculo central separadamente, mas a questão pede o momento de inércia da peça inteira que é uma placa quadrada com um furo.

Para calcular isso, é só tiramos do momento de inércia da placa quadrada a parte correspondente ao momento de inércia do círculo central:

I O = I O Q u a d r a d o - I O C i r c u l o

I O = 6,40 - 0,175  

I O = 6,23   k g . m 2  

Resposta

I O = 6,23   k g . m 2  

Exercícios de Livros Relacionados

Utilize os resultados do Prob. 7/55 e determine a quantidade de movimento angular H g dobrada daquele problema em relação ao seu centro de massa G utilizando os eixos de referência fornecidos.
A placa retangular, com uma massa de 3 kg e uma pequena espessura uniforme, está soldada no ângulo de 45º ao eixos vertical, que gira com a velocidade angular de 20 ⋅ πr a d / s . Determine a quantida
O mecanismo para controlar a implantação de um painel solar de uma nave espacial a partir da posição A para a posição B está sendo projetado. Determine a expressão vetorial para o único ângulo θ de ro
O pequeno motor M é articulado em relação ao eixo x através de O e transmite ao seu eixo AO uma velocidade constante p rad/s no sentido mostrado, em relação á sua carcaça. O conjunto inteiro é, em seg
O disco circular de 6 kg e o eixo associado giram a uma velocidade angular constante ω = 10000r p m . Se o centro de massa do disco está deslocado do centro em 0,05 mm, determine o módulo das forças h